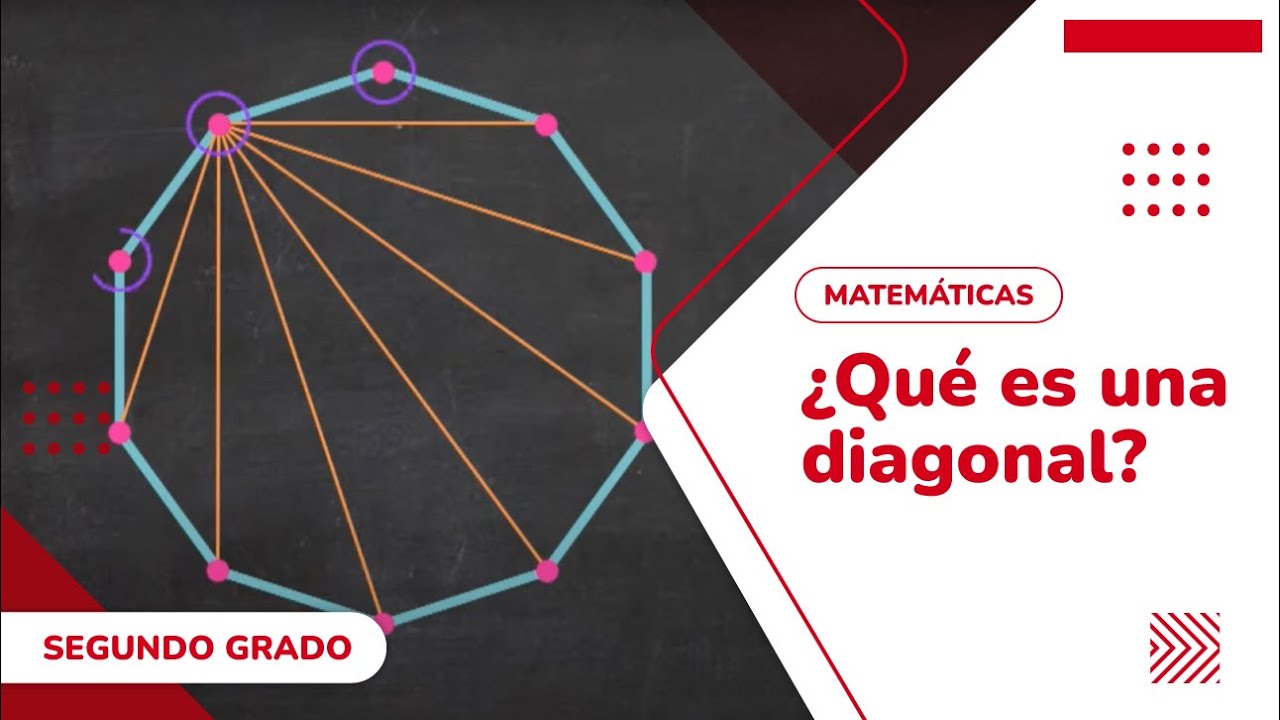
En matemáticas y geometría, una diagonal es una recta que une dos puntos no consecutivos de un polígono. Las diagonales pueden ser externas o internas. Las diagonales externas son aquellas que no están incluidas en el polígono, mientras que las diagonales internas son aquellas que sí están incluidas.
Definición
Una diagonal se define como una recta que une dos puntos no consecutivos de un polígono. Los puntos no consecutivos son aquellos que no están en la misma fila o columna.
Ejemplos
En el siguiente polígono, las diagonales son las líneas rojas y azules:
A / \ B C / \ D E En este caso, hay dos diagonales externas (AB y CD) y una diagonal interna (CE).
Tipos de diagonales
Las diagonales pueden clasificarse en dos tipos: externas e internas.
- Diagonales externas: Son aquellas que no están incluidas en el polígono.
- Diagonales internas: Son aquellas que sí están incluidas en el polígono.
Características de las diagonales
Las diagonales tienen las siguientes características:
- Pueden ser rectas o curvas.
- Pueden ser convergentes o divergentes.
- Pueden ser paralelas o perpendiculares.
Pendiente de una diagonal
La pendiente de una diagonal es la relación entre el cambio en el eje y el cambio en el eje x. Se puede calcular con la siguiente fórmula:
m = (y2 - y1) / (x2 - x1) donde:
- m es la pendiente
- y2 es la coordenada y del punto final
- y1 es la coordenada y del punto inicial
- x2 es la coordenada x del punto final
- x1 es la coordenada x del punto inicial
Diagonales en matrices
En matrices, las diagonales son las líneas que unen los elementos de la misma fila o columna. Las diagonales principales son las líneas que unen los elementos de la fila principal o la columna principal. Las diagonales secundarias son las líneas que unen los elementos de la fila secundaria o la columna secundaria.
Diagonales en cuadrículas
En cuadrículas, las diagonales son las líneas que unen dos puntos que no están en la misma fila o columna.
Diagonales en gráficos
En gráficos, las diagonales son las líneas que unen dos puntos de un gráfico.
Diagonales en diseño
En diseño, las diagonales se utilizan para crear un sentido de movimiento o tensión. También se pueden utilizar para crear un equilibrio o simetría.
Conclusión
Las diagonales son líneas importantes en matemáticas, geometría, matrices, cuadrículas, gráficos y diseño. Tienen una variedad de aplicaciones y pueden utilizarse para crear una variedad de efectos visuales.
diagonal, definición, matemáticas, geometría, recta, plano, paralelo, perpendicular, ángulo, pendiente, matriz, cuadrícula, gráfico, diseño, arte
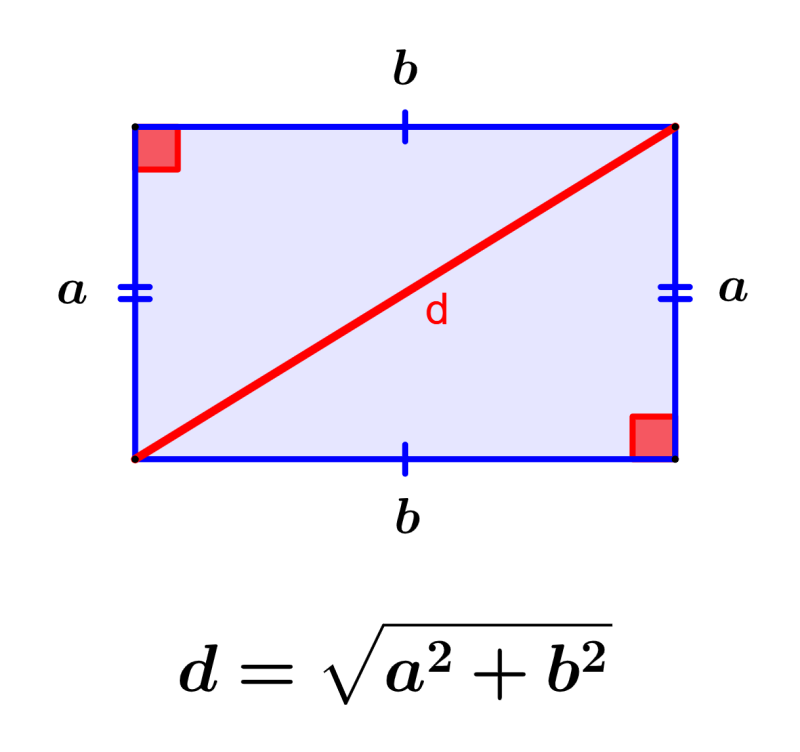
Diagonal de un Rectángulo – Fórmula y Ejercicios – Neurochispas

Source: Neurochispas
qué es una diagonal? – YouTube

Source: YouTube
Diagonal de un Cuadrado – Fórmulas y Ejercicios – Neurochispas
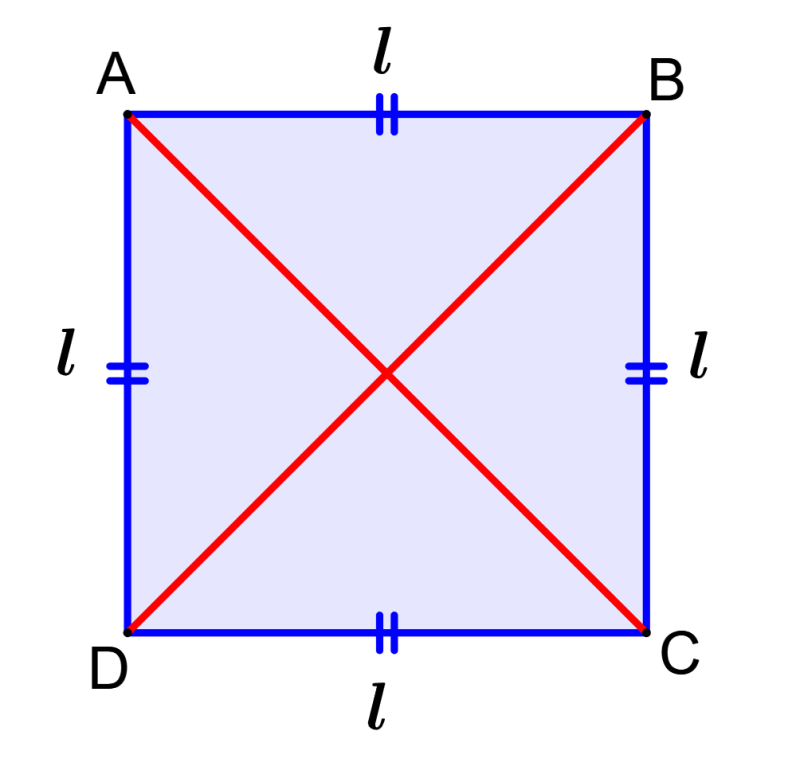
Source: Neurochispas
Que Es Una Diagonal, 15. ¿Qué es una diagonal, 7.03 MB, 05:07, 207,294, acervo – aprende_mx, 2019-10-18T19:25:02.000000Z, 2, Diagonal de un Rectángulo – Fórmula y Ejercicios – Neurochispas, Neurochispas, 752 x 800, jpg, , 3, que-es-una-diagonal, KAMPION
Que Es Una Diagonal.
Nivel: Telesecundaria
Grado: Segundo
Asignatura: Matemáticas
Bloque: 1
Secuencia: 8. Polígonos 1
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
¡Ayúdanos a mejorar nuestros contenidos!
Participa en nuestra encuesta y dinos qué opinas sobre el contenido de estos videos, lo que compartimos en redes sociales y los programas que transmitimos por el canal Ingenio, en el 14.2 de televisión abierta.
👉🏼 bit.ly/Encuesta-RED
Sigue las actividades de la Dirección General @prende.mx:
🌐 aprende.gob.mx/
📲 linktr.ee/aprende_mx