Viral Que Es La Diagonal Principal Y Secundaria De Una Matriz Nuevo

En matemáticas, una matriz es un conjunto de números dispuestos en filas y columnas. Las matrices se utilizan en una amplia gama de aplicaciones, desde la ciencia y la ingeniería hasta la economía y la finanzas.

En esta publicación de blog, veremos qué son la diagonal principal y secundaria de una matriz. También veremos cómo calcularlas y cómo se utilizan en matemáticas.

Diagonal principal

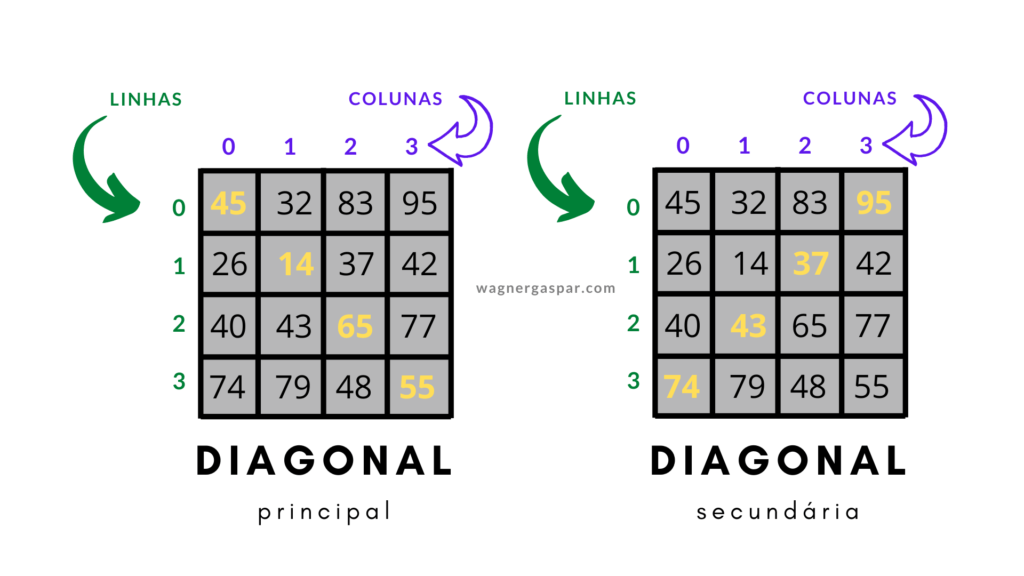
La diagonal principal de una matriz es la línea que va de la esquina superior izquierda a la esquina inferior derecha. Los elementos de la diagonal principal se denominan elementos diagonales.

Por ejemplo, la siguiente matriz tiene una diagonal principal de 1, 2, 3 y 4:

[1, 2, 3, 4] [5, 6, 7, 8] [9, 10, 11, 12] [13, 14, 15, 16] 

Diagonal secundaria

La diagonal secundaria de una matriz es la línea que va de la esquina superior derecha a la esquina inferior izquierda. Los elementos de la diagonal secundaria se denominan elementos secundarios.

Por ejemplo, la siguiente matriz tiene una diagonal secundaria de 5, 6, 7 y 8:

[1, 2, 3, 4] [5, 6, 7, 8] [9, 10, 11, 12] [13, 14, 15, 16] 

Cálculo de la diagonal principal y secundaria

La diagonal principal y secundaria de una matriz se pueden calcular de forma sencilla.

Para calcular la diagonal principal, se puede utilizar la siguiente fórmula:

diagonal_principal = [a_11, a_22, ..., a_nn] 

donde:

• a_ij es el elemento de la matriz en la fila i y la columna j
• n es el número de filas de la matriz

Por ejemplo, para calcular la diagonal principal de la matriz anterior, utilizaríamos la siguiente fórmula:

diagonal_principal = [1, 6, 11, 16] 

Para calcular la diagonal secundaria, se puede utilizar la siguiente fórmula:

diagonal_secundaria = [a_n1, a_n2, ..., a_1n] 

donde:

• a_ij es el elemento de la matriz en la fila i y la columna j
• n es el número de filas de la matriz

Por ejemplo, para calcular la diagonal secundaria de la matriz anterior, utilizaríamos la siguiente fórmula:

diagonal_secundaria = [5, 10, 15, 20] 

Uso de la diagonal principal y secundaria

La diagonal principal y secundaria de una matriz se utilizan en una amplia gama de aplicaciones matemáticas.

Por ejemplo, la diagonal principal se utiliza para calcular la determinante de una matriz. El determinante de una matriz es un número que se utiliza para determinar si una matriz es invertible.

La diagonal secundaria se utiliza para calcular la traza de una matriz. La traza de una matriz es la suma de los elementos de la diagonal principal.

Además, la diagonal principal y secundaria se utilizan en una variedad de algoritmos de álgebra lineal, como el método de Gauss-Jordan y el método de la potencia.

Conclusión

La diagonal principal y secundaria de una matriz son dos conceptos importantes en matemáticas. Son utilizados en una amplia gama de aplicaciones, desde la ciencia y la ingeniería hasta la economía y las finanzas.

• diagonal principal

• diagonal secundaria

• matriz

• determinante

• traza

• álgebra lineal

• método de Gauss-Jordan

• método de la potencia

• fila

• columna

• elemento

• número

• fórmula

Que Es La Diagonal Principal Y Secundaria De Una Matriz, Matriz 04: Diagonal Principal e Secundaria de uma Matriz, 3.85 MB, 02:48, 49,466, Matemática no Papel, 2020-03-27T01:56:52.000000Z, 2, Como imprimir a diagonal principal e secundária de uma matriz em Portugol – Wagner Gaspar, Wagner Gaspar, 576 x 1024, jpg, , 3, que-es-la-diagonal-principal-y-secundaria-de-una-matriz, KAMPION

Que Es La Diagonal Principal Y Secundaria De Una Matriz.

Aula ministrada pelo professor Ítalo Benfica.

Siga o instagram @matematicanopapel

Matriz 04: Diagonal Principal e Secundaria de uma Matriz

Como imprimir a diagonal principal e secundária de uma matriz em Portugol – Wagner Gaspar

Que Es La Diagonal Principal Y Secundaria De Una Matriz,