
En geometría, una diagonal es un segmento de recta que une dos vértices no consecutivos de un polígono o de un poliedro. En el caso de un rombo, las diagonales son dos segmentos que se cortan en ángulos rectos y que pasan por el centro del rombo.
La diagonal mayor de un rombo es la diagonal que tiene mayor longitud. La diagonal menor es la diagonal que tiene menor longitud.
La diagonal mayor de un rombo se define como el segmento de recta que une dos vértices opuestos del rombo, pasando por el centro del mismo.
La diagonal mayor de un rombo se representa con la letra d.
La diagonal mayor de un rombo tiene las siguientes propiedades:
- Es la diagonal de mayor longitud del rombo.
- Corta al rombo en dos triángulos isósceles congruentes.
- Es perpendicular a la diagonal menor.
El cálculo de la diagonal mayor de un rombo se puede realizar de varias maneras.
Una forma de calcular la diagonal mayor es utilizando el teorema de Pitágoras.
Si a y b son las longitudes de los lados del rombo, entonces la diagonal mayor se calcula de la siguiente manera:
d^2 = a^2 + b^2 Otra forma de calcular la diagonal mayor es utilizando la siguiente fórmula:
d = √(2 * p * q) Donde:
- p es la semisuma de las longitudes de los lados del rombo.
- q es la distancia entre los centros de las dos diagonales.
Ejemplo 1
Consideremos un rombo con lados de longitud 5 cm.
En este caso, la diagonal mayor se calcula de la siguiente manera:
d^2 = 5^2 + 5^2 d^2 = 50 d = √50 d = 7.07 cm Ejemplo 2
Consideremos un rombo con semisuma de las longitudes de los lados de 6 cm y distancia entre los centros de las dos diagonales de 4 cm.
En este caso, la diagonal mayor se calcula de la siguiente manera:
d = √(2 * 6 * 4) d = √48 d = 4 * √3 d = 12√3 cm La diagonal mayor de un rombo es un segmento de recta que tiene una longitud mayor que la diagonal menor. Tiene varias propiedades, como cortar al rombo en dos triángulos isósceles congruentes y ser perpendicular a la diagonal menor.
El cálculo de la diagonal mayor se puede realizar de varias maneras, como utilizando el teorema de Pitágoras o la siguiente fórmula:
d = √(2 * p * q) Donde:
-
p es la semisuma de las longitudes de los lados del rombo.
-
q es la distancia entre los centros de las dos diagonales.
-
diagonal mayor
-
rombo
-
teorema de Pitágoras
-
semisuma de las longitudes de los lados
-
distancia entre los centros de las dos diagonales
-
diagonal
-
polígono
-
poliedro
-
ángulo recto
-
centro
-
longitud
-
congruente
-
isósceles
-
perpendicular
-
cálculo
Diagonal de un rombo – Qué es, definición y concepto | 2023 | Economipedia

Source: Economipedia
Área del rombo – Desafíos matemáticos

Source: Desafíos matemáticos – WordPress.com
Fórmula del área de triángulos y cuadriláteros – Nueva Escuela Mexicana
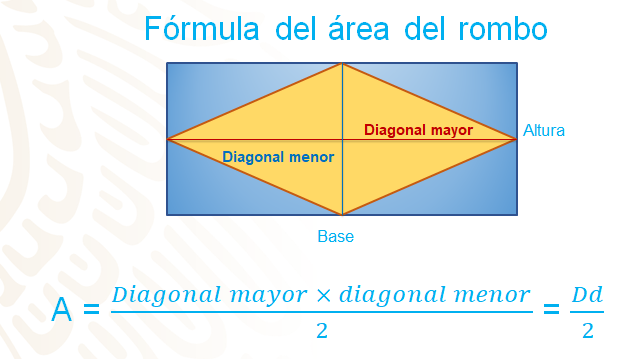
Source: Nueva Escuela Mexicana
Que Significa Diagonal Mayor, 1139 – Pregunta resuelta sobre la diagonal mayor y diagonal menor en el rombo, 1.85 MB, 01:21, 86, Profesor peruano, 2022-07-08T15:56:11.000000Z, 2, Diagonal de un rombo – Qué es, definición y concepto | 2023 | Economipedia, Economipedia, 1000 x 619, jpg, , 3, que-significa-diagonal-mayor, KAMPION
Que Significa Diagonal Mayor.
DESARROLLO GRÁFICO
Traza la diagonal mayor (D) y la diagonal menor (d) en este rombo.
[ imágenes del rombo en el video ]
Espero el video te resulte entretenido y sigas visitando otros videos del canal.
Diagonal de un rombo – Qué es, definición y concepto | 2023 | Economipedia
1139 – Pregunta resuelta sobre la diagonal mayor y diagonal menor en el rombo

Source: Youtube.com
184. 2do Calcular la diagonal Mayor de un ROMBO
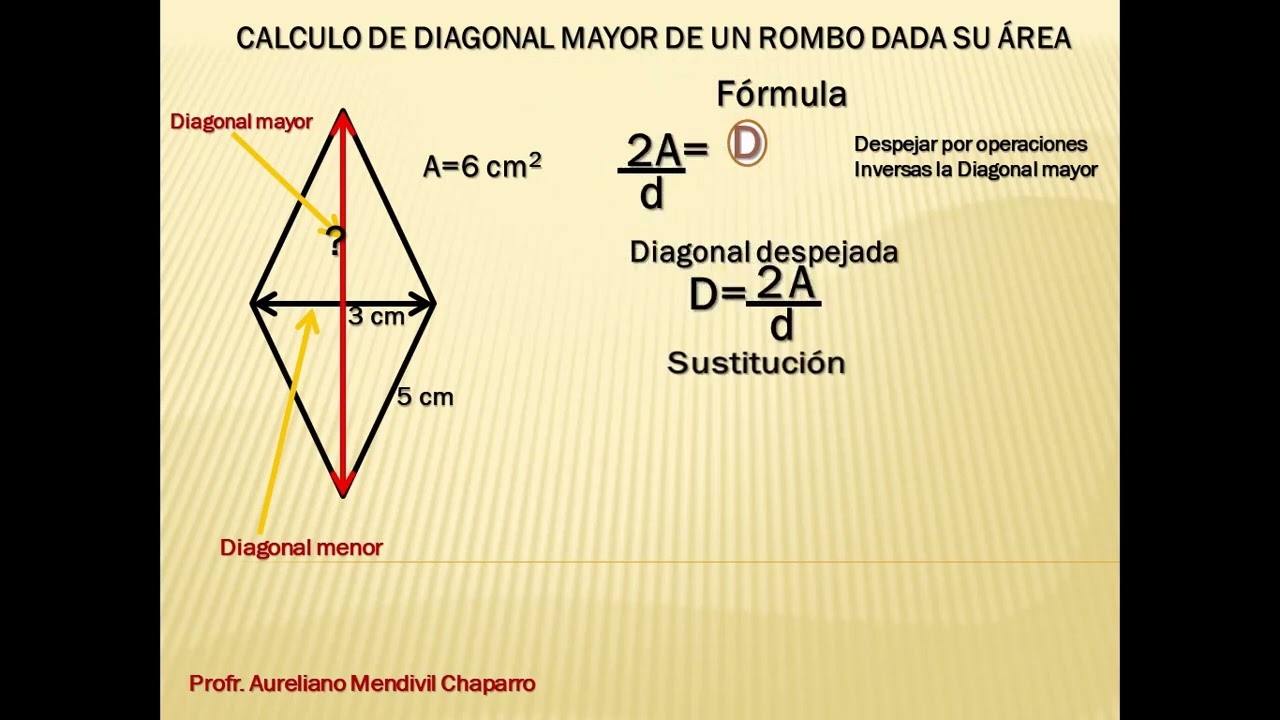
Source: Youtube.com