Acerca de Qué Significa Diagonal A

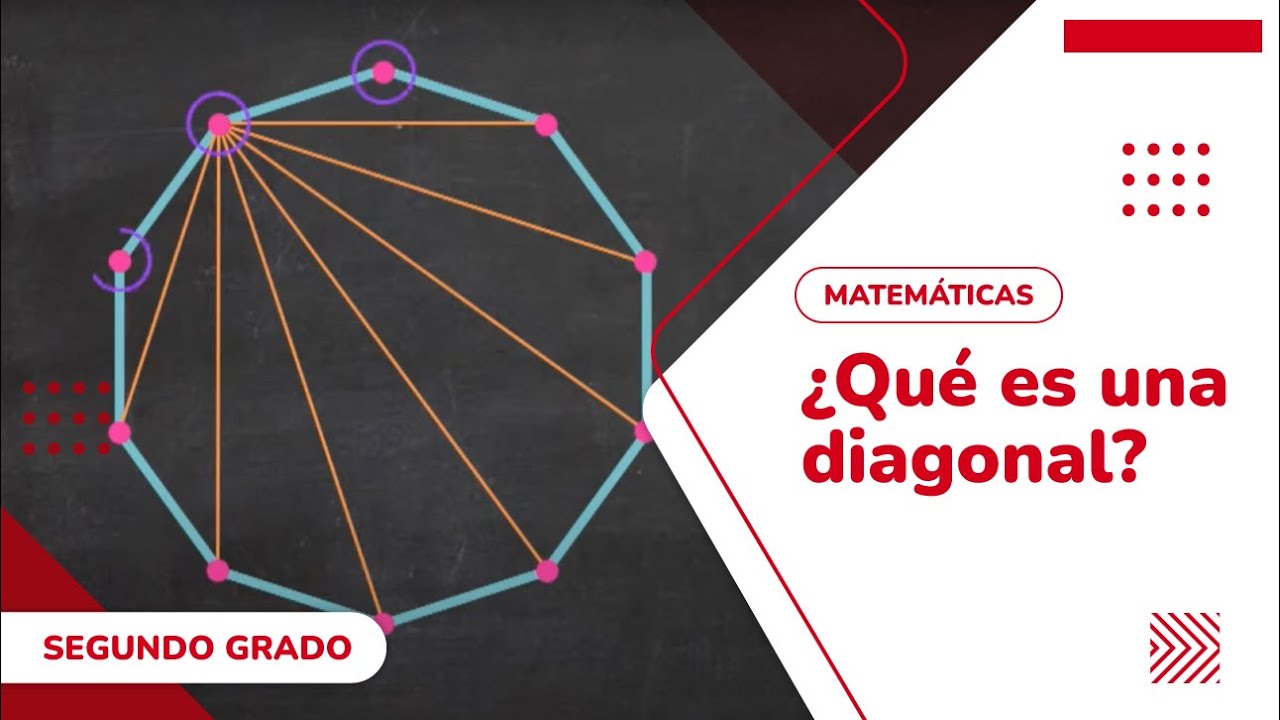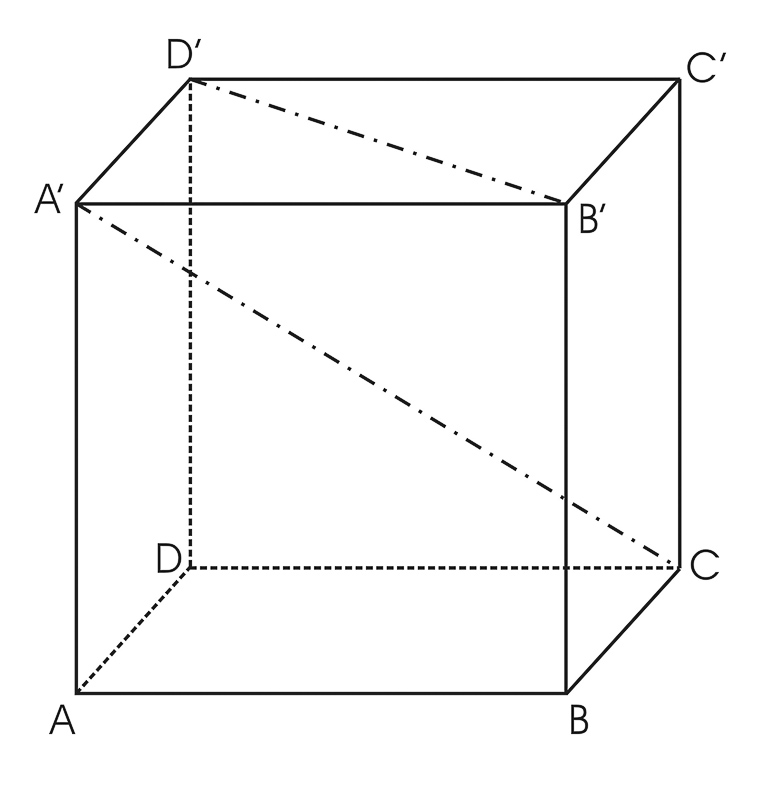
La palabra "diagonal" se utiliza en una variedad de contextos, pero tiene un significado específico en matemáticas. En este contexto, una diagonal es una línea recta que une dos vértices no consecutivos de un polígono o de un poliedro.

En esta publicación de blog, exploraremos el significado de la diagonal A en detalle. Primero, definiremos la diagonal A en términos matemáticos. Luego, veremos algunos ejemplos de diagonales A en diferentes tipos de polígonos y poliedros. Finalmente, discutiremos algunas aplicaciones de las diagonales A en matemáticas y en la vida cotidiana.

Definición de la diagonal A

En matemáticas, una diagonal A es una línea recta que une dos vértices no consecutivos de un polígono o de un poliedro. En otras palabras, una diagonal A es una línea recta que no es un lado del polígono o poliedro.

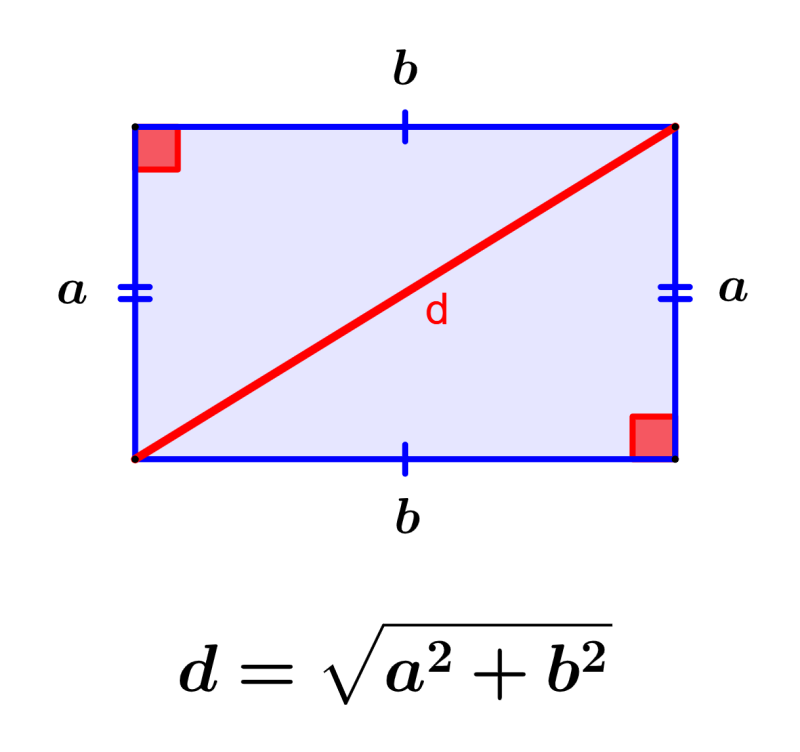
La longitud de una diagonal A se puede calcular utilizando la siguiente fórmula:

L = √(x² + y²) 

donde:

• L es la longitud de la diagonal A
• x es la distancia desde el primer vértice al punto de intersección de la diagonal A con un lado del polígono o poliedro
• y es la distancia desde el segundo vértice al punto de intersección de la diagonal A con el mismo lado

Ejemplos de diagonales A

En un cuadrado, hay dos diagonales A. Estas diagonales son perpendiculares entre sí y tienen la misma longitud.

En un rectángulo, hay dos diagonales A. Estas diagonales son congruentes, pero no son perpendiculares entre sí.

En un triángulo, puede haber una o dos diagonales A. Si el triángulo es equilátero, hay dos diagonales A que son congruentes y perpendiculares entre sí.

En un pentágono, hay cinco diagonales A.

En un hexágono, hay nueve diagonales A.

Aplicaciones de las diagonales A

Las diagonales A tienen una variedad de aplicaciones en matemáticas y en la vida cotidiana.

En matemáticas, las diagonales A se utilizan para calcular el área de un polígono. Por ejemplo, la fórmula para calcular el área de un cuadrado con diagonal A es la siguiente:

A = √2 * L² 

donde:

• A es el área del cuadrado
• L es la longitud de la diagonal A

Las diagonales A también se utilizan para calcular el volumen de un poliedro. Por ejemplo, la fórmula para calcular el volumen de un cubo con diagonal A es la siguiente:

V = L³ / 3√2 

donde:

• V es el volumen del cubo
• L es la longitud de la diagonal A

En la vida cotidiana, las diagonales A se utilizan en una variedad de aplicaciones, como:

• La construcción de puentes y edificios
• El diseño de circuitos electrónicos
• El desarrollo de juegos y aplicaciones informáticas

Conclusión

En esta publicación de blog, hemos explorado el significado de la diagonal A en detalle. Hemos definido la diagonal A en términos matemáticos, visto algunos ejemplos de diagonales A en diferentes tipos de polígonos y poliedros, y discutido algunas aplicaciones de las diagonales A en matemáticas y en la vida cotidiana.

• diagonal A
• definición de diagonal A
• ejemplos de diagonales A
• aplicaciones de las diagonales A

Qué Significa Diagonal A, 15. ¿Qué es una diagonal, 7.03 MB, 05:07, 207,294, acervo – aprende_mx, 2019-10-18T19:25:02.000000Z, 2, DIAGONAL – Definición y sinónimos de diagonal en el diccionario español, Educalingo, 800 x 770, jpg, , 3, que-significa-diagonal-a, KAMPION

Qué Significa Diagonal A.

Nivel: Telesecundaria
Grado: Segundo
Asignatura: Matemáticas
Bloque: 1
Secuencia: 8. Polígonos 1

– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –

¡Ayúdanos a mejorar nuestros contenidos!

Participa en nuestra encuesta y dinos qué opinas sobre el contenido de estos videos, lo que compartimos en redes sociales y los programas que transmitimos por el canal Ingenio, en el 14.2 de televisión abierta.

👉🏼 bit.ly/Encuesta-RED

Sigue las actividades de la Dirección General @prende.mx:

🌐 aprende.gob.mx/
📲 linktr.ee/aprende_mx

DIAGONAL – Definición y sinónimos de diagonal en el diccionario español

Qué Significa Diagonal A,