Descifrando el significado de "Diagonal": Un viaje a través de la geometría y la matemática
La palabra "diagonal" resuena con diversos significados en el ámbito de la geometría, la matemática y el lenguaje cotidiano. Si bien su uso coloquial se refiere a cualquier línea inclinada o sesgada, en el mundo de las formas y los números, la diagonal adquiere una definición más precisa y amplia. Embárcate en un viaje de exploración para comprender a fondo el significado de "diagonal" en sus diferentes contextos.
1. Diagonal en geometría: Un enlace entre vértices
En el reino de la geometría, una diagonal se define como un segmento de línea que une dos vértices no consecutivos de una figura plana, como un polígono o un poliedro. En otras palabras, es una línea que corta a través de una figura, conectando dos puntos que no están adyacentes entre sí.
2. Tipos de diagonales: Una clasificación geométrica
Las diagonales se clasifican según el tipo de figura a la que pertenecen. En un polígono, una diagonal une cualquier par de vértices que no sean adyacentes, sin importar su posición relativa. Por ejemplo, en un cuadrado, todas las diagonales tienen la misma longitud, mientras que en un triángulo, solo existe una diagonal posible.
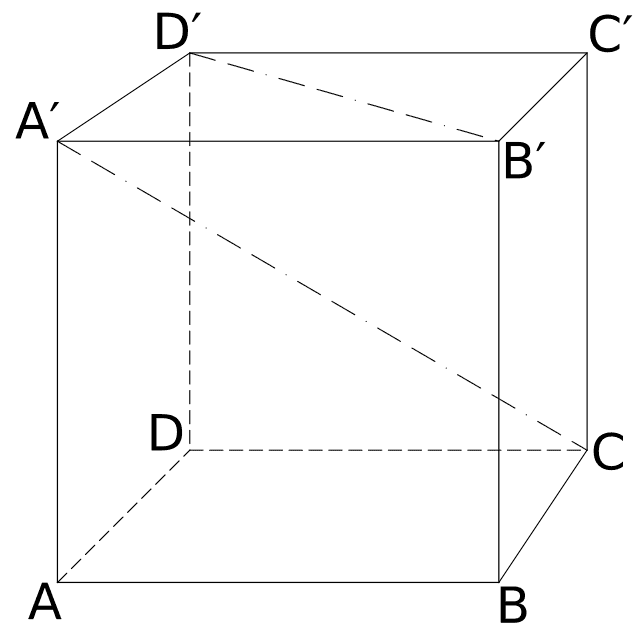
En el caso de los poliedros, las diagonales conectan vértices opuestos de una cara o cruzan a través de caras adyacentes. Por ejemplo, en un cubo, las diagonales de una cara forman un triángulo equilátero, mientras que las diagonales que atraviesan caras adyacentes forman ángulos rectos.
3. Propiedades de las diagonales: Explorando relaciones geométricas
Las diagonales poseen propiedades geométricas interesantes que dependen del tipo de figura a la que pertenecen. En un polígono convexo, todas las diagonales se encuentran dentro de la figura, mientras que en un polígono cóncavo, algunas diagonales pueden quedar fuera de la figura.
Además, las diagonales pueden dividir una figura en partes más pequeñas, creando nuevas formas y relaciones geométricas. Por ejemplo, en un paralelogramo, las diagonales bisectan los ángulos opuestos y dividen la figura en cuatro triángulos equivalentes.
4. Diagonales en la matriz diagonal: Una estructura matemática especial
En el ámbito de las matrices, una matriz diagonal es un tipo especial de matriz cuadrada en la que solo los elementos de la diagonal principal son distintos de cero, mientras que los demás elementos son todos ceros. Esta estructura simplifica considerablemente las operaciones matemáticas con matrices diagonales.
Las matrices diagonales se utilizan en diversas aplicaciones, como la representación de sistemas de ecuaciones lineales, la solución de problemas de autovalores y la descomposición de matrices más complejas. Su simplicidad y propiedades únicas las convierten en herramientas valiosas en el campo del álgebra lineal.
5. La diagonal en el lenguaje cotidiano: Una inclinación significativa
En el lenguaje cotidiano, la palabra "diagonal" se utiliza para referirse a cualquier línea o camino que se inclina o se desvía de una dirección horizontal o vertical. Por ejemplo, una calle diagonal es aquella que corta a través de un patrón de calles paralelas, creando una intersección en ángulo.
Esta acepción coloquial de "diagonal" refleja la idea de una línea que se aleja de lo regular o lo convencional, aportando una dimensión oblicua a la percepción del espacio. De esta manera, la diagonal se convierte en una metáfora de la diversidad y la no conformidad.
6. Conclusión: Una palabra con múltiples significados
La palabra "diagonal" posee un significado rico y diverso, abarcando tanto conceptos geométricos precisos como usos coloquiales más informales. Desde las diagonales que conectan vértices en figuras planas hasta las matrices diagonales que simplifican cálculos matemáticos, la diagonal se manifiesta como un elemento fundamental en diferentes áreas del conocimiento.
Su presencia en el lenguaje cotidiano, como sinónimo de inclinación o desviación, añade una dimensión simbólica a este concepto matemático. La diagonal representa la ruptura con lo establecido, la exploración de nuevas perspectivas y la búsqueda de caminos alternativos.
Diagonal – Wikiwand

Source: Wikiwand
Diagonal – Wikiwand

Source: Wikiwand
Método diagonal – Wikiwand
Source: Wikiwand
Que Es Diagonal Wikipedia, Como calcular la DIAGONAL de un RECTANGULO, 9.13 MB, 06:39, 82,332, Felipe Delgado, 2021-09-08T16:00:24.000000Z, 2, Diagonal – Wikiwand, Wikiwand, 635 x 640, jpg, , 3, que-es-diagonal-wikipedia, KAMPION
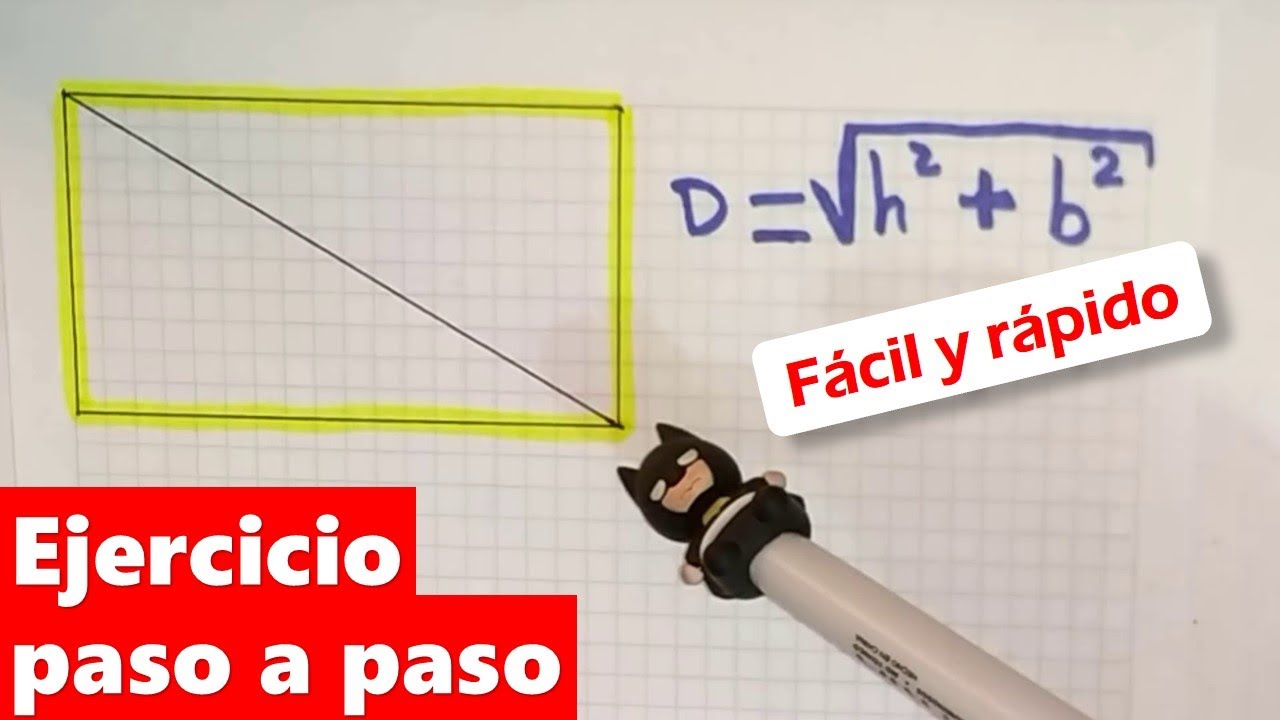
Que Es Diagonal Wikipedia.
Aprende como calcular la diagonal de un rectángulo con el teorema de Pitágoras mirando este ejercicio resuelto y explicado paso a paso. Calcular las diagonales de un rectángulo también se conoce como la hipotenusa de un rectángulo.
Sígueme en mis demás redes sociales para más contenido que te puede ayudar
Instagram 👉 instagram.com/lfelipe0307/
Twitter 👉 twitter.com/lFelipe_10
TikTok 👉 tiktok.com/@lfelipe0307
Pinterest 👉 pinterest.es/lfelipe0307
Facebook 👉 facebook.com/profile.php?id=100076995576179
BLOG 👉 aprendemascrecemas.blogspot.com.co/
Bibliografía: Geometría 5 ed. Daniel C. Alexander & Geralyn M. Koeberlein.
universoformulas.com/matematicas/geometria/diagonales-rectangulo/
es.wikipedia.org/wiki/Hipotenusa#:~:text=La%20hipotenusa%20es%20el%20lado,su%20lado%20de%20mayor%20longitud.
es.wikipedia.org/wiki/Teorema_de_Pit%C3%A1goras
Álgebra de Baldor. Aurelio Baldor.
Aritmetica: Teorico‑Practica. Aurelio Baldor.
#FelipeDelgado #Matematicas #Geometria
INDICE
00:00 Introducción
00:20 Que es una diagonal
00:55 Diagonal de un rectangulo formula
02:00 Ejercicio diagonal de un rectángulo
06:19 Mas ejercicios de matematicas