
Una matriz diagonal es una matriz cuadrada en la que todos los elementos que no están en la diagonal principal son cero. La diagonal principal es la línea que va de la esquina superior izquierda a la esquina inferior derecha de la matriz.
Definición
Una matriz diagonal se define como una matriz cuadrada en la que todos los elementos que no están en la diagonal principal son cero. La diagonal principal es la línea que va de la esquina superior izquierda a la esquina inferior derecha de la matriz.
Ejemplo
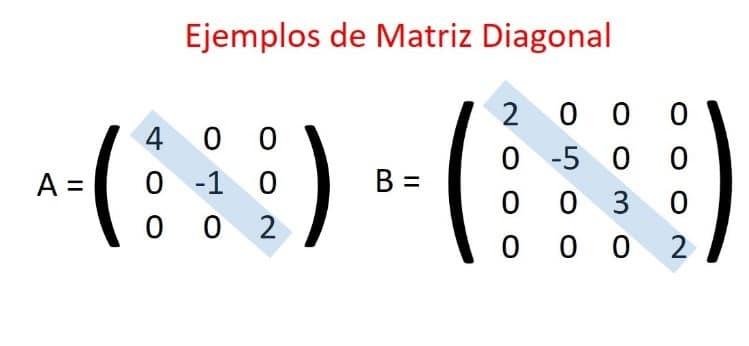
La siguiente matriz es una matriz diagonal:
[1 0 0] [0 2 0] [0 0 3] En esta matriz, todos los elementos que no están en la diagonal principal son cero. Los elementos de la diagonal principal son 1, 2 y 3.
Propiedades
Las matrices diagonales tienen varias propiedades importantes:
- La suma de dos matrices diagonales es otra matriz diagonal.
- El producto de dos matrices diagonales es otra matriz diagonal.
- La inversa de una matriz diagonal es otra matriz diagonal.
Aplicaciones
Las matrices diagonales tienen muchas aplicaciones en matemáticas, ciencia e ingeniería. Por ejemplo, se utilizan en:
- El análisis de sistemas lineales
- El cálculo de determinantes
- La solución de ecuaciones lineales
- La representación de sistemas físicos
Ejemplos de aplicaciones
Las matrices diagonales se utilizan en una variedad de aplicaciones, como:
- El análisis de sistemas lineales: Las matrices diagonales se pueden utilizar para representar sistemas lineales que tienen componentes independientes. Por ejemplo, una matriz diagonal se puede utilizar para representar el movimiento de un sistema de masas unidas por resortes.
- El cálculo de determinantes: Las matrices diagonales se pueden utilizar para simplificar el cálculo de determinantes. Por ejemplo, el determinante de una matriz diagonal es simplemente el producto de los elementos de la diagonal principal.
- La solución de ecuaciones lineales: Las matrices diagonales se pueden utilizar para resolver sistemas de ecuaciones lineales. Por ejemplo, una matriz diagonal se puede utilizar para resolver un sistema de ecuaciones lineales que tiene la forma Ax = b.
- La representación de sistemas físicos: Las matrices diagonales se pueden utilizar para representar sistemas físicos que tienen componentes independientes. Por ejemplo, una matriz diagonal se puede utilizar para representar el movimiento de un sistema de partículas que están interconectadas por fuerzas elásticas.
Conclusión
Las matrices diagonales son una herramienta importante en matemáticas, ciencia e ingeniería. Tienen una variedad de propiedades y aplicaciones que las hacen útiles para una variedad de problemas.
09 Matriz Diagonal.mp4 – YouTube

Source: YouTube
Matriz triangular – Qué es, definición y concepto | 2023 | Economipedia

Source: Economipedia
Sumando conocimiento,Restando Ignorancia y Multiplicando Logros by Luz Mariely Hernandez Ulloa – Issuu
Source: Issuu
Que Es Matriz Diagonal Y Ejemplo, MATRIZ DIAGONAL, 2.68 MB, 01:57, 24,022, Profe Santiago Velasquez, 2019-09-13T03:52:50.000000Z, 2, 09 Matriz Diagonal.mp4 – YouTube, YouTube, 360 x 480, jpg, , 3, que-es-matriz-diagonal-y-ejemplo, KAMPION
Que Es Matriz Diagonal Y Ejemplo.
09 Matriz Diagonal.mp4 – YouTube
MATRIZ DIAGONAL
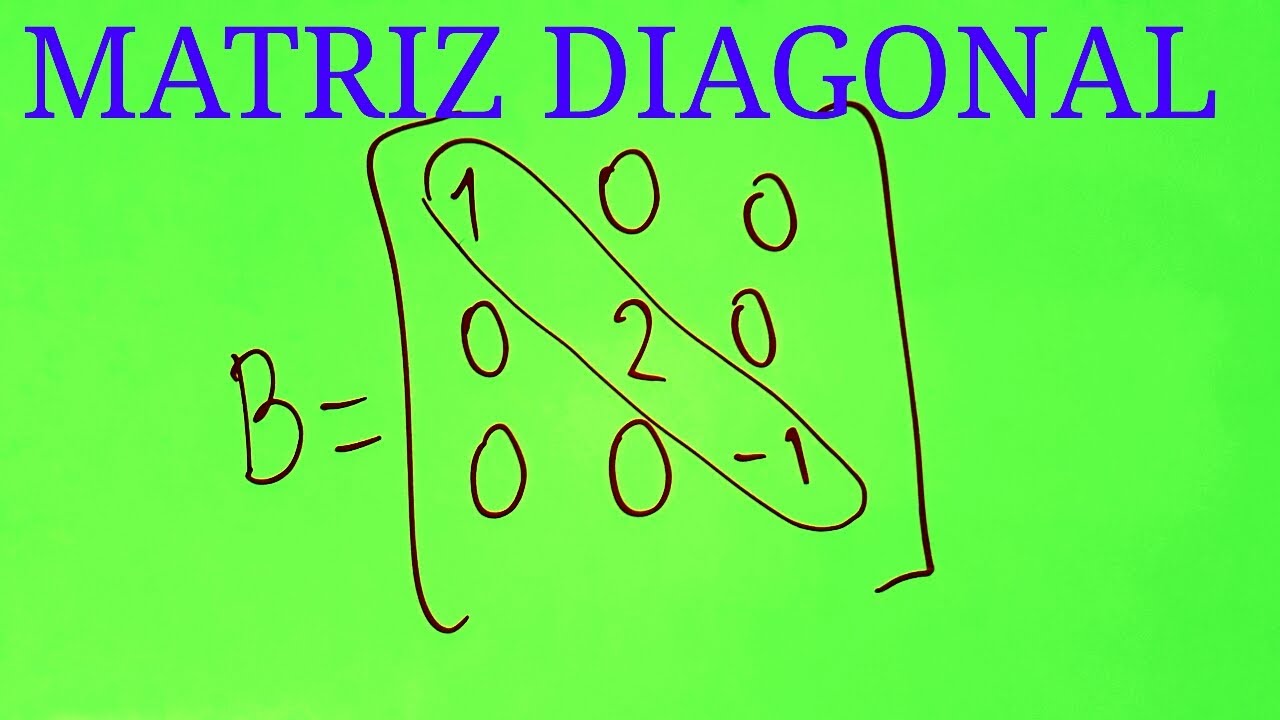
Source: Youtube.com
🤔¿Qué es una matriz diagonal🤔 Tipos de MATRICES #matematicas #matrices Suscríbete 👇👇👇
Source: Youtube.com