
En matemáticas, una matriz diagonal es una matriz en la que todos los elementos fuera de la diagonal principal son cero. La diagonal principal es la línea de elementos que va de la esquina superior izquierda a la esquina inferior derecha de la matriz.
Las matrices diagonales tienen una serie de propiedades que las hacen útiles en una variedad de aplicaciones. Por ejemplo, son fáciles de multiplicar y sus inversas se pueden calcular fácilmente.
Definición
Una matriz diagonal es una matriz cuadrada en la que todos los elementos fuera de la diagonal principal son cero. La diagonal principal es la línea de elementos que va de la esquina superior izquierda a la esquina inferior derecha de la matriz.
Una matriz diagonal se puede escribir en la siguiente forma:
A = diag(a1, a2, ..., an) donde a1, a2, …, an son los elementos de la diagonal principal.
Ejemplos
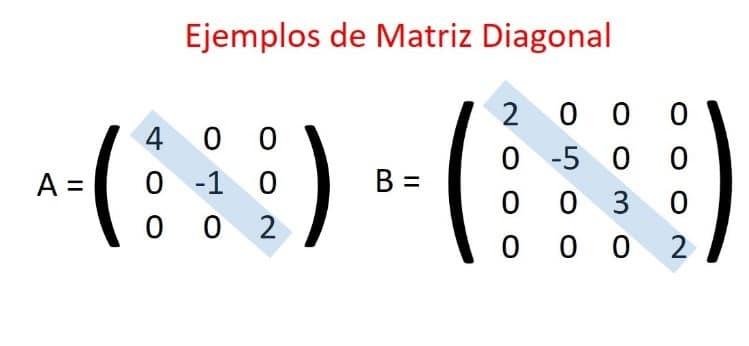
Aquí hay algunos ejemplos de matrices diagonales:
A = [1 0 0; 0 2 0; 0 0 3] B = [4 0 0; 0 5 0; 0 0 6] C = [7 0 0; 0 8 0; 0 0 9] Todas estas matrices son cuadradas, y todos los elementos fuera de la diagonal principal son cero.
Propiedades
Las matrices diagonales tienen una serie de propiedades que las hacen útiles en una variedad de aplicaciones.
Multiplicación
La multiplicación de matrices diagonales es muy sencilla. La siguiente fórmula se aplica a cualquier matriz diagonal A y B de dimensiones iguales:
AB = diag(a1*b1, a2*b2, ..., an*bn) Por ejemplo, si A = diag(1, 2, 3) y B = diag(4, 5, 6), entonces AB = diag(4, 10, 18).
Inversa
La inversa de una matriz diagonal también es muy sencilla de calcular. La siguiente fórmula se aplica a cualquier matriz diagonal A:
A^-1 = diag(1/a1, 1/a2, ..., 1/an) Por ejemplo, si A = diag(1, 2, 3), entonces A^-1 = diag(1/1, 1/2, 1/3).
Aplicaciones
Las matrices diagonales se utilizan en una variedad de aplicaciones, incluyendo:
- Álgebra lineal: Las matrices diagonales se utilizan en muchos problemas de álgebra lineal, como la resolución de sistemas de ecuaciones lineales, el cálculo de determinantes y la transformación de matrices.
- Física: Las matrices diagonales se utilizan en física para representar sistemas dinámicos lineales, como osciladores armónicos y circuitos eléctricos.
- Química: Las matrices diagonales se utilizan en química para representar sistemas moleculares, como moléculas de diatómicos y polímeros.
- Economía: Las matrices diagonales se utilizan en economía para representar sistemas económicos, como los modelos de oferta y demanda.
Conclusión
Las matrices diagonales son una herramienta importante en matemáticas y ciencias. Son fáciles de multiplicar y sus inversas se pueden calcular fácilmente. Estas propiedades las hacen útiles en una variedad de aplicaciones.
-
matriz diagonal
-
definición
-
ejemplos
-
propiedades
-
aplicaciones
-
matriz diagonal: matriz, diagonal, cuadrado, elemento, fuera, diagonal principal, fórmula, multiplicar, inversa
-
definición: matriz diagonal, definición, diagonal, cuadrado, elemento, fuera, diagonal principal
-
ejemplos: matriz diagonal, ejemplos, diagonal, cuadrado, elemento, fuera, diagonal principal
-
propiedades: matriz diagonal, propiedades, multiplicación, inversa
-
aplicaciones: matriz diagonal, aplicaciones, álgebra lineal, física, química, economía
09 Matriz Diagonal.mp4 – YouTube

Source: YouTube
Matriz triangular – Qué es, definición y concepto | 2023 | Economipedia

Source: Economipedia
Sumando conocimiento,Restando Ignorancia y Multiplicando Logros by Luz Mariely Hernandez Ulloa – Issuu
Source: Issuu
Que Es Matriz Diagonal Ejemplos, MATRIZ DIAGONAL, 2.68 MB, 01:57, 24,022, Profe Santiago Velasquez, 2019-09-13T03:52:50.000000Z, 2, 09 Matriz Diagonal.mp4 – YouTube, YouTube, 360 x 480, jpg, , 3, que-es-matriz-diagonal-ejemplos, KAMPION
Que Es Matriz Diagonal Ejemplos.
09 Matriz Diagonal.mp4 – YouTube
MATRIZ DIAGONAL
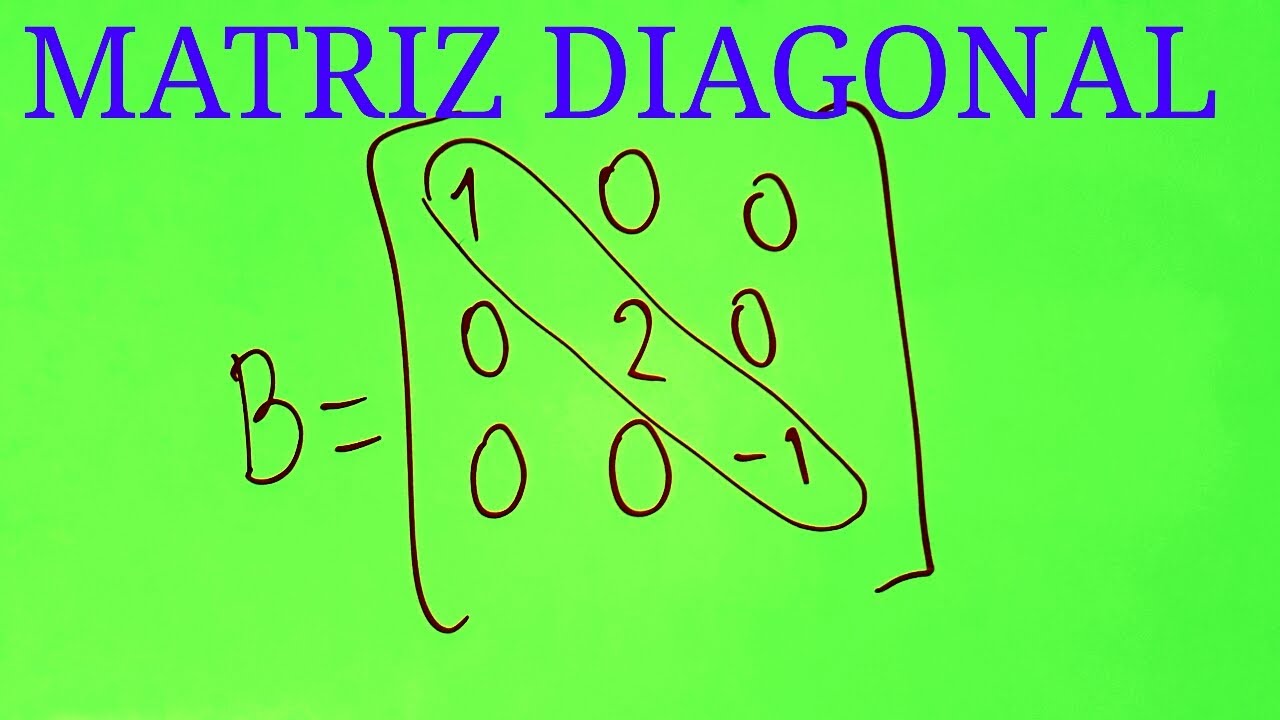
Source: Youtube.com
🤔¿Qué es una matriz diagonal🤔 Tipos de MATRICES #matematicas #matrices Suscríbete 👇👇👇
Source: Youtube.com