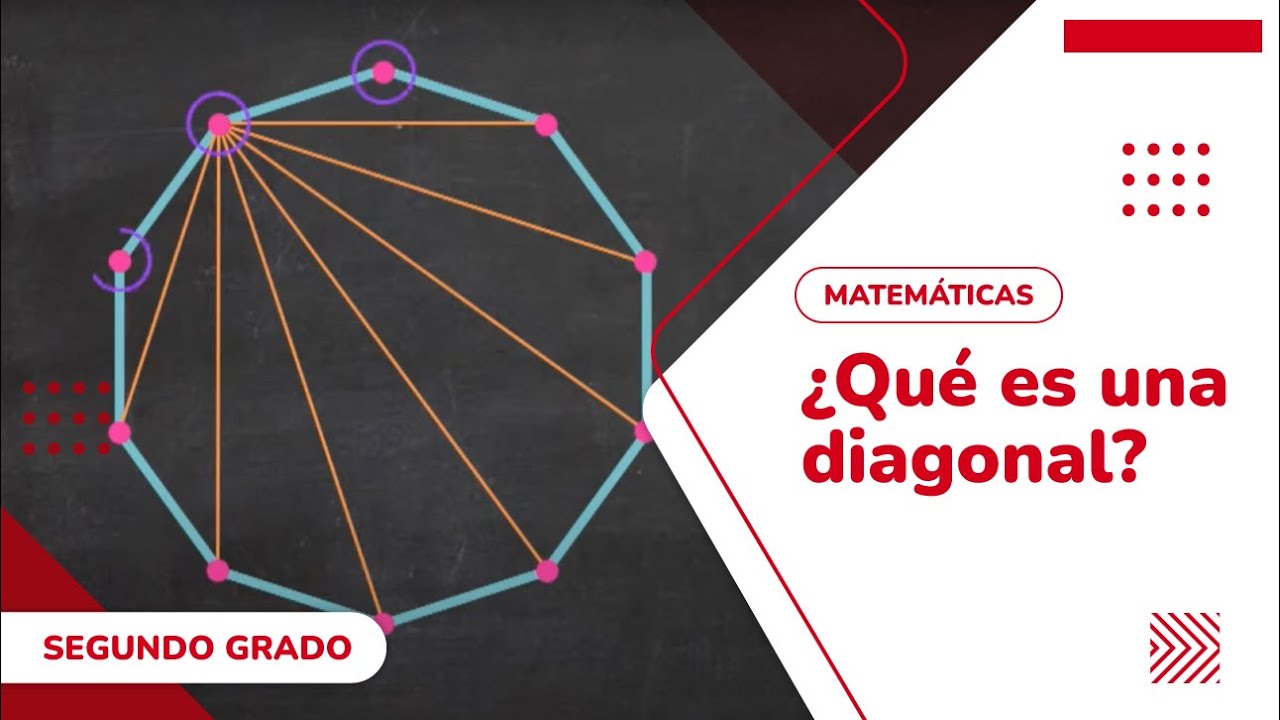
En matemáticas, una diagonal es un segmento de recta que une dos vértices no consecutivos de un polígono o de un poliedro. En otras palabras, una diagonal es un segmento de recta que no es una arista del polígono o poliedro.
Definición
La definición de diagonal es la siguiente:
Diagonal: Segmento de recta que une dos vértices no consecutivos de un polígono o de un poliedro.
Ejemplos
En el siguiente polígono, las diagonales son los segmentos de recta que unen los vértices 1 y 3, 1 y 4, 2 y 4, y 3 y 4.
1-------2-------3 / | \ / | \ 4 5 6 7 En el siguiente poliedro, las diagonales son los segmentos de recta que unen los vértices A y C, A y D, B y C, B y D, C y E, y D y E.
A---B---C / | \ / | \ D E F Clasificación de diagonales
Las diagonales se pueden clasificar según el número de vértices que atraviesan. De esta manera, tenemos las siguientes categorías:
- Diagonales internas: Diagonales que atraviesan dos vértices que pertenecen a la misma cara del polígono o poliedro.
- Diagonales externas: Diagonales que atraviesan dos vértices que pertenecen a caras distintas del polígono o poliedro.
En el siguiente polígono, las diagonales internas son las que unen los vértices 1 y 3, 1 y 4, y 2 y 4. Las diagonales externas son las que unen los vértices 1 y 5, 1 y 6, 2 y 5, 2 y 6, 3 y 5, y 3 y 6.
1-------2-------3 / | \ / | \ 4 5 6 7 En el siguiente poliedro, las diagonales internas son las que unen los vértices A y C, A y D, B y C, B y D, y C y E. Las diagonales externas son las que unen los vértices A y F, B y F, C y F, D y F, E y F.
A---B---C / | \ / | \ D E F Cálculo del número de diagonales
El número de diagonales que se pueden trazar en un polígono se puede calcular mediante la siguiente fórmula:
N = n (n - 3) / 2 donde:
- N es el número de diagonales
- n es el número de lados del polígono
Por ejemplo, un triángulo tiene 3 lados, por lo que el número de diagonales que se pueden trazar es:
N = 3 (3 - 3) / 2 = 0 En consecuencia, un triángulo no tiene diagonales.
Un cuadrado tiene 4 lados, por lo que el número de diagonales que se pueden trazar es:
N = 4 (4 - 3) / 2 = 2 En consecuencia, un cuadrado tiene 2 diagonales.
Un pentágono tiene 5 lados, por lo que el número de diagonales que se pueden trazar es:
N = 5 (5 - 3) / 2 = 5 En consecuencia, un pentágono tiene 5 diagonales.
Y así sucesivamente.
Conclusiones
Una diagonal es un segmento de recta que une dos vértices no consecutivos de un polígono o de un poliedro. Las diagonales se pueden clasificar según el número de vértices que atraviesan. El número de diagonales que se pueden trazar en un polígono se puede calcular mediante la siguiente fórmula:
N = n (n - 3) / 2 -
diagonal
-
polígono
-
poliedro
-
vértice
-
arista
-
interno
-
externo
-
número de diagonales
-
fórmula
-
segmento
-
recta
-
segmento de recta
-
no consecutivos
-
no consecutivos
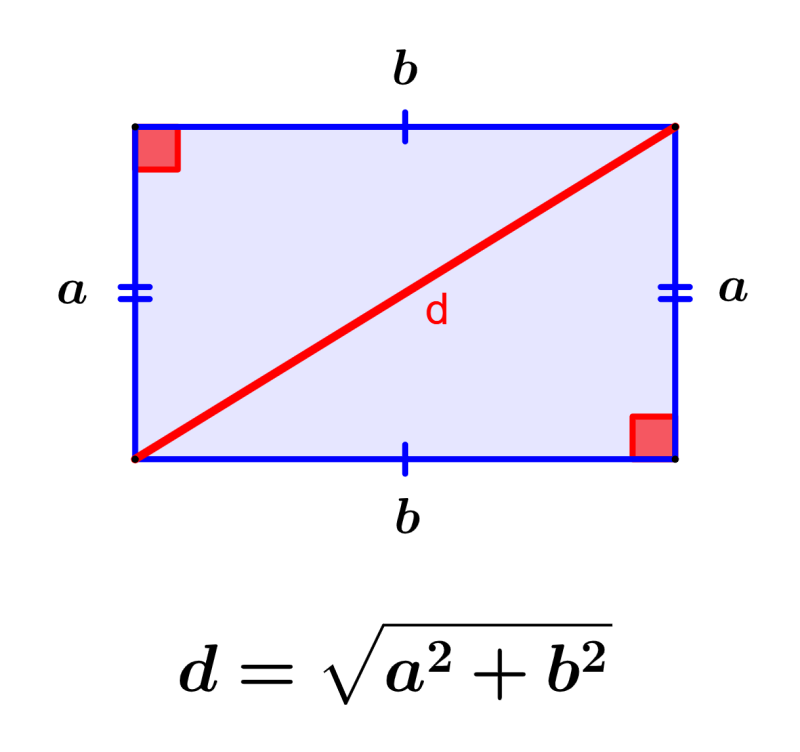
Diagonal de un Rectángulo – Fórmula y Ejercicios – Neurochispas

Source: Neurochispas
Calcular la Diagonal de un Rectángulo – YouTube

Source: YouTube
Diagonal de un Cuadrado – Fórmulas y Ejercicios – Neurochispas
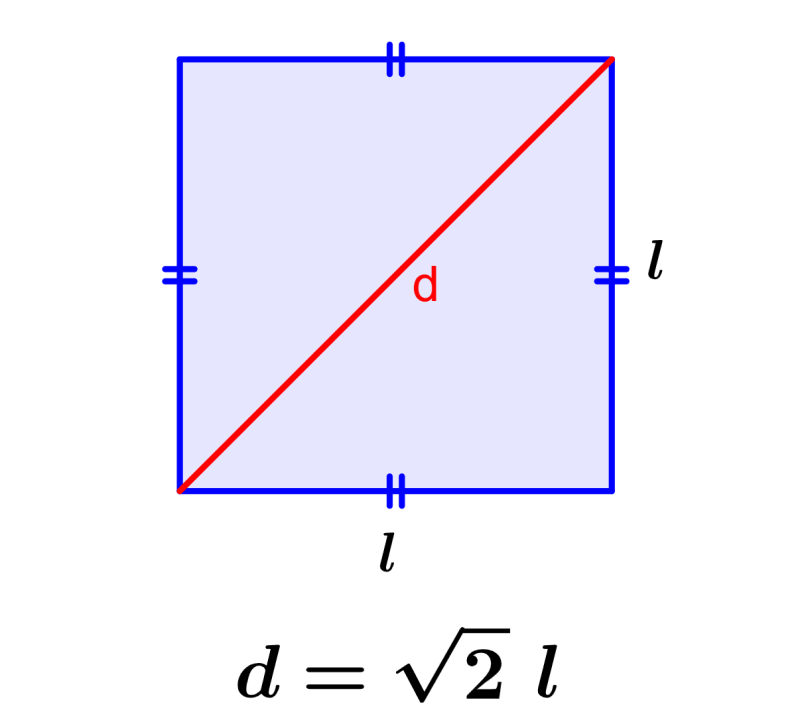
Source: Neurochispas
Que Es La Diagonal En Matematicas, ¿qué es una diagonal, 11.24 MB, 08:11, 23,290, El profe Meny MATEMÁTICAS, 2020-11-18T21:41:03.000000Z, 2, Diagonal de un Rectángulo – Fórmula y Ejercicios – Neurochispas, Neurochispas, 752 x 800, jpg, , 3, que-es-la-diagonal-en-matematicas, KAMPION
Que Es La Diagonal En Matematicas.
se explica el concepto matemático de la diagonal y la forma de calcular cuántas diagonales cuenta los polígonos