
En matemáticas, una diagonal es una línea recta que une dos puntos no adyacentes de una figura geométrica. Las diagonales pueden ser internas o externas. Las diagonales internas son las que se encuentran dentro de la figura geométrica, mientras que las diagonales externas son las que se encuentran fuera de la figura geométrica.
Tipos de diagonales
Existen diferentes tipos de diagonales, dependiendo de la figura geométrica de la que se trate.
- Diagonal principal: es la diagonal que une dos vértices opuestos de un rectángulo o un cuadrado.
- Diagonal secundaria: es la diagonal que une dos vértices no opuestos de un rectángulo o un cuadrado.
- Diagonal de una matriz: es la línea recta que une dos elementos no adyacentes de una matriz.
- Diagonal de un polígono: es la línea recta que une dos vértices no adyacentes de un polígono.
- Diagonal de un cuadrado: es la línea recta que une dos vértices opuestos de un cuadrado.
- Diagonal de un rectángulo: es la línea recta que une dos vértices opuestos de un rectángulo.
- Diagonal de un triángulo: es la línea recta que une dos vértices no adyacentes de un triángulo.
Ejemplos de diagonales
A continuación se presentan algunos ejemplos de diagonales:
- En un rectángulo, la diagonal principal es la línea que une los vértices superior izquierdo y inferior derecho. La diagonal secundaria es la línea que une los vértices superior derecho e inferior izquierdo.
[Imagen de un rectángulo con sus diagonales]
- En un cuadrado, la diagonal principal y la diagonal secundaria son las mismas.
[Imagen de un cuadrado con su diagonal]
- En una matriz, la diagonal principal es la línea que une los elementos de la primera fila con los elementos de la última columna. La diagonal secundaria es la línea que une los elementos de la primera columna con los elementos de la última fila.
[Imagen de una matriz con sus diagonales]
- En un polígono, la diagonal es cualquier línea recta que une dos vértices no adyacentes.
[Imagen de un polígono con sus diagonales]
- En un cuadrado, las diagonales son las únicas diagonales que se pueden trazar.
[Imagen de un cuadrado con sus diagonales]
- En un rectángulo, se pueden trazar dos diagonales.
[Imagen de un rectángulo con sus diagonales]
- En un triángulo, se pueden trazar hasta tres diagonales.
[Imagen de un triángulo con sus diagonales]
Conclusiones
Las diagonales son líneas rectas que pueden tener diferentes funciones, dependiendo de la figura geométrica de la que se trate. En algunos casos, las diagonales pueden ayudar a dividir una figura geométrica en dos partes iguales. En otros casos, las diagonales pueden ayudar a crear patrones o diseños.
diagonal, línea diagonal, diagonal principal, diagonal secundaria, diagonal de una matriz, diagonal de un polígono, diagonal de un cuadrado, diagonal de un rectángulo, diagonal de un triángulo
Cómo calcular cuántas diagonales tiene un polígono

Source: wikiHow
Diagonales de un trapecio isósceles | Tutorela
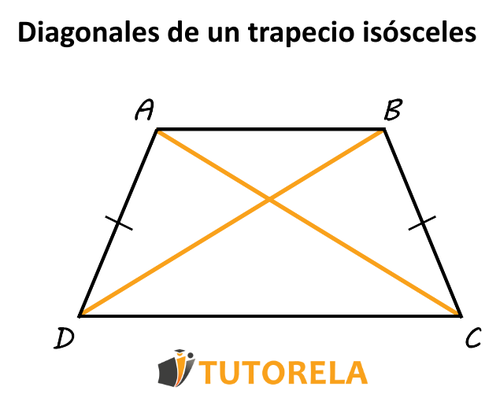
Source: Tutorela
Diagonal – Qué es, origen, definición y concepto

Source: Definición.de
Que Es Diagonal Y Dar Ejemplos, 15. ¿Qué es una diagonal, 7.03 MB, 05:07, 207,294, acervo – aprende_mx, 2019-10-18T19:25:02.000000Z, 2, Cómo calcular cuántas diagonales tiene un polígono, wikiHow, 345 x 460, jpg, , 3, que-es-diagonal-y-dar-ejemplos, KAMPION
Que Es Diagonal Y Dar Ejemplos.
Nivel: Telesecundaria
Grado: Segundo
Asignatura: Matemáticas
Bloque: 1
Secuencia: 8. Polígonos 1
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
¡Ayúdanos a mejorar nuestros contenidos!
Participa en nuestra encuesta y dinos qué opinas sobre el contenido de estos videos, lo que compartimos en redes sociales y los programas que transmitimos por el canal Ingenio, en el 14.2 de televisión abierta.
👉🏼 bit.ly/Encuesta-RED
Sigue las actividades de la Dirección General @prende.mx:
🌐 aprende.gob.mx/
📲 linktr.ee/aprende_mx
Cómo calcular cuántas diagonales tiene un polígono
15. ¿Qué es una diagonal
Source: Youtube.com
Cantidad de DIAGONALES de un POLÍGONO – BUENISIMO
Source: Youtube.com