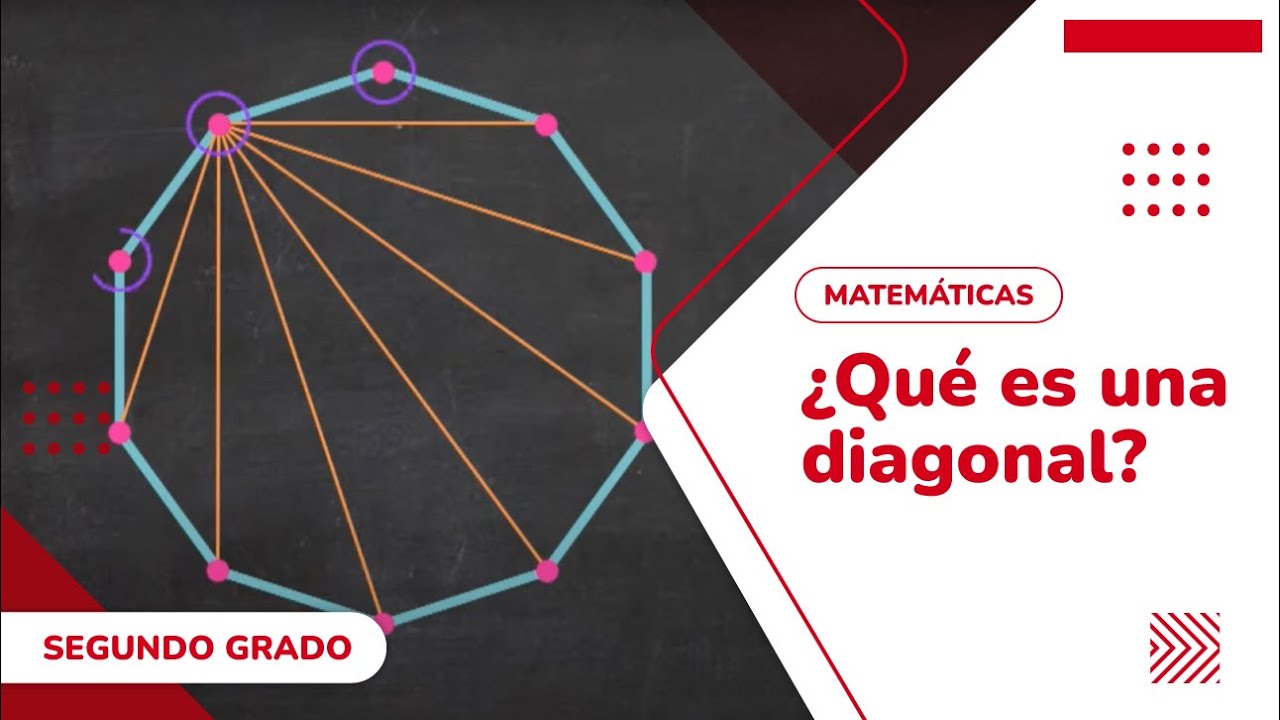
En aritmética, una diagonal es un segmento de recta que une dos vértices no consecutivos de un polígono o de un poliedro. En sentido coloquial, una diagonal es una recta o segmento con cierta inclinación o un conjunto de elementos alineados de esta manera.
Definición formal
Más formalmente, una diagonal de un polígono es un segmento de recta que une dos vértices no adyacentes o no consecutivos. En otras palabras, una diagonal es un segmento de recta que no es un lado del polígono.
Ejemplos
En el siguiente diagrama, se muestran las diagonales del triángulo equilátero.
[Diagrama de un triángulo equilátero con sus diagonales]
Las diagonales del triángulo equilátero son los segmentos de recta que unen los vértices no adyacentes. En este caso, hay tres diagonales:
- Diagonal 1: Une los vértices A y C.
- Diagonal 2: Une los vértices B y C.
- Diagonal 3: Une los vértices A y B.
Cálculo del número de diagonales
El número de diagonales de un polígono se puede calcular mediante la siguiente fórmula:
Nd = n(n - 3) / 2 donde:
- Nd es el número de diagonales.
- n es el número de lados del polígono.
Por ejemplo, el triángulo equilátero tiene tres lados, por lo que el número de diagonales se calcula como sigue:
Nd = 3(3 - 3) / 2 Nd = 3(0) / 2 Nd = 0 Por lo tanto, el triángulo equilátero no tiene diagonales.
Ejemplos de diagonales en la aritmética
Las diagonales se utilizan en muchas áreas de la aritmética, incluyendo:
- Geometría: Las diagonales se utilizan para calcular el área y el perímetro de polígonos.
- Trigonometría: Las diagonales se utilizan para resolver triángulos oblicuos.
- Álgebra: Las diagonales se utilizan para resolver sistemas de ecuaciones lineales.
Conclusión
En conclusión, una diagonal es un segmento de recta que une dos vértices no consecutivos de un polígono o de un poliedro. Las diagonales tienen muchas aplicaciones en la aritmética, incluyendo la geometría, la trigonometría y el álgebra.
-
diagonal
-
aritmética
-
geometría
-
trigonometría
-
álgebra
-
polígono
-
poliedro
-
vértice
-
segmento
-
recta
-
En la introducción:En aritmética, una diagonal es un segmento de recta que une dos vértices no consecutivos de un polígono o de un poliedro.
-
En el cuerpo de la publicación:El número de diagonales de un polígono se puede calcular mediante la siguiente fórmula: Nd = n(n – 3) / 2.
-
En la conclusión:En conclusión, las diagonales tienen muchas aplicaciones en la aritmética, incluyendo la geometría, la trigonometría y el álgebra.
-
Definición formal
-
Ejemplos
-
Cálculo del número de diagonales
-
Ejemplos de diagonales en la aritmética
-
Conclusión
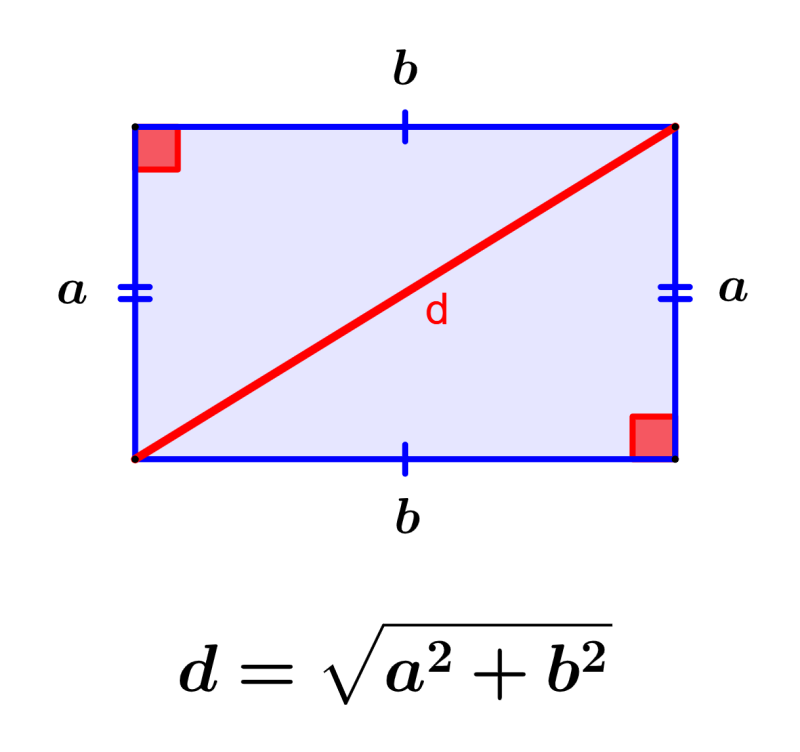
Diagonal de un Rectángulo – Fórmula y Ejercicios – Neurochispas

Source: Neurochispas
Como calcular la DIAGONAL de un RECTANGULO – YouTube

Source: YouTube
qué es una diagonal? – YouTube

Source: YouTube
Que Es Diagonal En Aritmetica, ¿qué es una diagonal, 11.24 MB, 08:11, 23,290, El profe Meny MATEMÁTICAS, 2020-11-18T21:41:03.000000Z, 2, Diagonal de un Rectángulo – Fórmula y Ejercicios – Neurochispas, Neurochispas, 752 x 800, jpg, , 3, que-es-diagonal-en-aritmetica, KAMPION
Que Es Diagonal En Aritmetica.
se explica el concepto matemático de la diagonal y la forma de calcular cuántas diagonales cuenta los polígonos