En la física, el término "diagonal" se utiliza para referirse a una línea recta que une dos puntos no consecutivos de una figura geométrica. En el caso de las figuras planas, las diagonales pueden ser internas o externas. Las diagonales internas son aquellas que se encuentran dentro de la figura, mientras que las diagonales externas son aquellas que se encuentran fuera de la figura.
Diagonales internas
Las diagonales internas de una figura plana son aquellas que unen dos vértices no consecutivos de la figura. Por ejemplo, en un triángulo, las diagonales internas son las líneas que unen los vértices no consecutivos del triángulo.
Las diagonales internas de una figura plana pueden tener diversas propiedades, dependiendo de la figura en cuestión. Por ejemplo, en un triángulo equilátero, las diagonales internas son congruentes. En un cuadrado, las diagonales internas son perpendiculares entre sí.
Diagonales externas
Las diagonales externas de una figura plana son aquellas que unen dos vértices no consecutivos de la figura, pero que no se encuentran dentro de la figura. Por ejemplo, en un triángulo, las diagonales externas son las líneas que unen los vértices no consecutivos del triángulo, pero que no se encuentran dentro del triángulo.
Las diagonales externas de una figura plana también pueden tener diversas propiedades, dependiendo de la figura en cuestión. Por ejemplo, en un triángulo equilátero, las diagonales externas son congruentes. En un cuadrado, las diagonales externas son paralelas entre sí.
Diagonales en cuerpos geométricos
En el caso de los cuerpos geométricos, el término "diagonal" se utiliza para referirse a una línea recta que une dos puntos no consecutivos de la figura. En el caso de los poliedros, las diagonales pueden ser internas o externas. Las diagonales internas son aquellas que se encuentran dentro del cuerpo geométrico, mientras que las diagonales externas son aquellas que se encuentran fuera del cuerpo geométrico.
Diagonales internas
Las diagonales internas de un cuerpo geométrico son aquellas que unen dos vértices no consecutivos del cuerpo geométrico. Por ejemplo, en un cubo, las diagonales internas son las líneas que unen los vértices no consecutivos del cubo.
Las diagonales internas de un cuerpo geométrico pueden tener diversas propiedades, dependiendo del cuerpo geométrico en cuestión. Por ejemplo, en un cubo, las diagonales internas son congruentes.
Diagonales externas
Las diagonales externas de un cuerpo geométrico son aquellas que unen dos vértices no consecutivos del cuerpo geométrico, pero que no se encuentran dentro del cuerpo geométrico. Por ejemplo, en un cubo, las diagonales externas son las líneas que unen los vértices no consecutivos del cubo, pero que no se encuentran dentro del cubo.
Las diagonales externas de un cuerpo geométrico también pueden tener diversas propiedades, dependiendo del cuerpo geométrico en cuestión. Por ejemplo, en un cubo, las diagonales externas son perpendiculares entre sí.
- diagonal
- física
- figura geométrica
- polígono
- poliedro
- vértice
- arista
- segmento
- recta
- perpendicular
- paralelo
- congruente
- interior
- exterior
Conclusión
En conclusión, el término "diagonal" se utiliza en física para referirse a una línea recta que une dos puntos no consecutivos de una figura geométrica. Las diagonales pueden ser internas o externas, dependiendo de si se encuentran dentro o fuera de la figura. Las diagonales pueden tener diversas propiedades, dependiendo de la figura en cuestión.
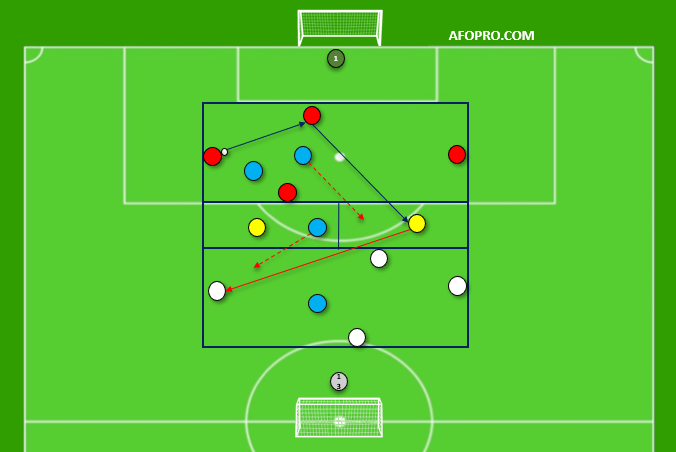
Diagonales: Propuesta de entrenamiento para su mejora

Source: AFOPRO
Diagonal de un Rectángulo – Fórmula y Ejercicios – Neurochispas
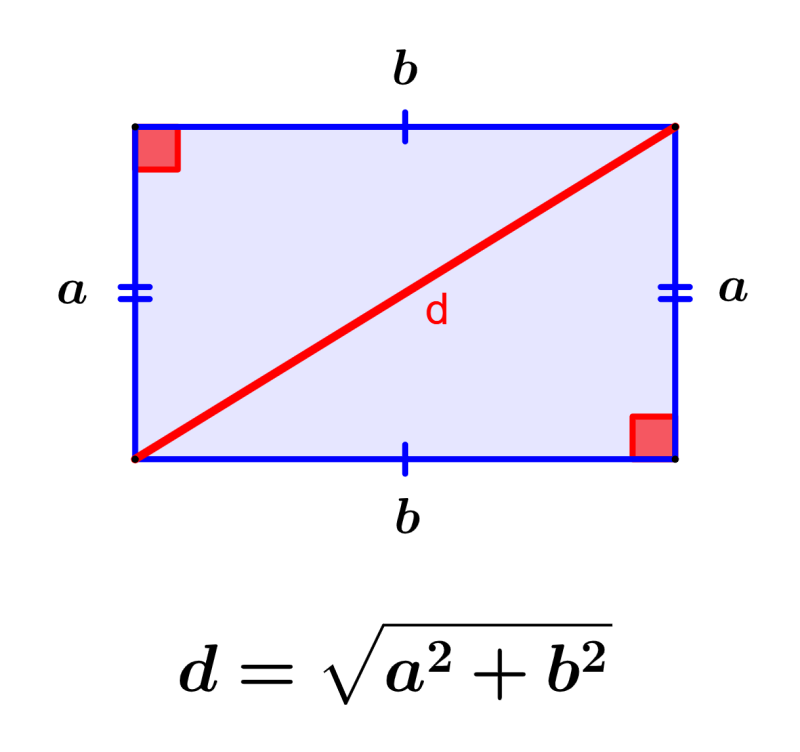
Source: Neurochispas
Diagonales con carrera contínua: Ejercicio Físico en EntrenamientosDe
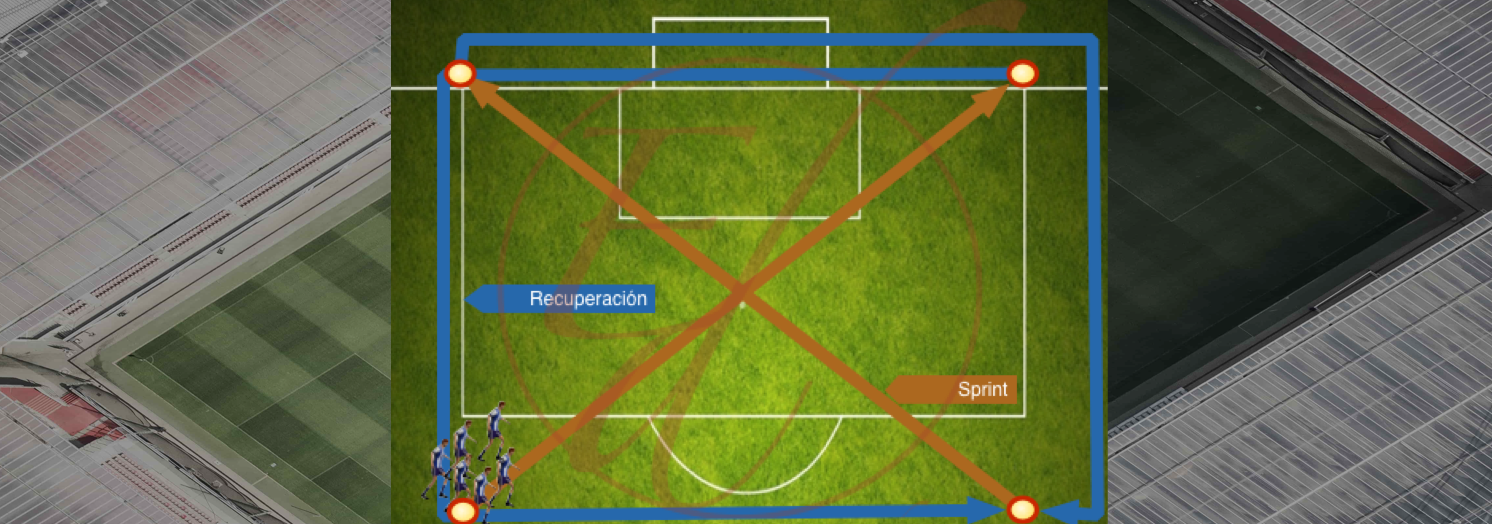
Source: Entrenamientos De
Que Significa Diagonal En Fisica, Como calcular la DIAGONAL de un RECTANGULO, 9.13 MB, 06:39, 82,332, Felipe Delgado, 2021-09-08T16:00:24.000000Z, 2, Diagonales: Propuesta de entrenamiento para su mejora, AFOPRO, 452 x 676, jpg, , 3, que-significa-diagonal-en-fisica, KAMPION
Que Significa Diagonal En Fisica.
Aprende como calcular la diagonal de un rectángulo con el teorema de Pitágoras mirando este ejercicio resuelto y explicado paso a paso. Calcular las diagonales de un rectángulo también se conoce como la hipotenusa de un rectángulo.
Sígueme en mis demás redes sociales para más contenido que te puede ayudar
Instagram 👉 instagram.com/lfelipe0307/
Twitter 👉 twitter.com/lFelipe_10
TikTok 👉 tiktok.com/@lfelipe0307
Pinterest 👉 pinterest.es/lfelipe0307
Facebook 👉 facebook.com/profile.php?id=100076995576179
BLOG 👉 aprendemascrecemas.blogspot.com.co/
Bibliografía: Geometría 5 ed. Daniel C. Alexander & Geralyn M. Koeberlein.
universoformulas.com/matematicas/geometria/diagonales-rectangulo/
es.wikipedia.org/wiki/Hipotenusa#:~:text=La%20hipotenusa%20es%20el%20lado,su%20lado%20de%20mayor%20longitud.
es.wikipedia.org/wiki/Teorema_de_Pit%C3%A1goras
Álgebra de Baldor. Aurelio Baldor.
Aritmetica: Teorico‑Practica. Aurelio Baldor.
#FelipeDelgado #Matematicas #Geometria
INDICE
00:00 Introducción
00:20 Que es una diagonal
00:55 Diagonal de un rectangulo formula
02:00 Ejercicio diagonal de un rectángulo
06:19 Mas ejercicios de matematicas
Diagonales: Propuesta de entrenamiento para su mejora
Como calcular la DIAGONAL de un RECTANGULO
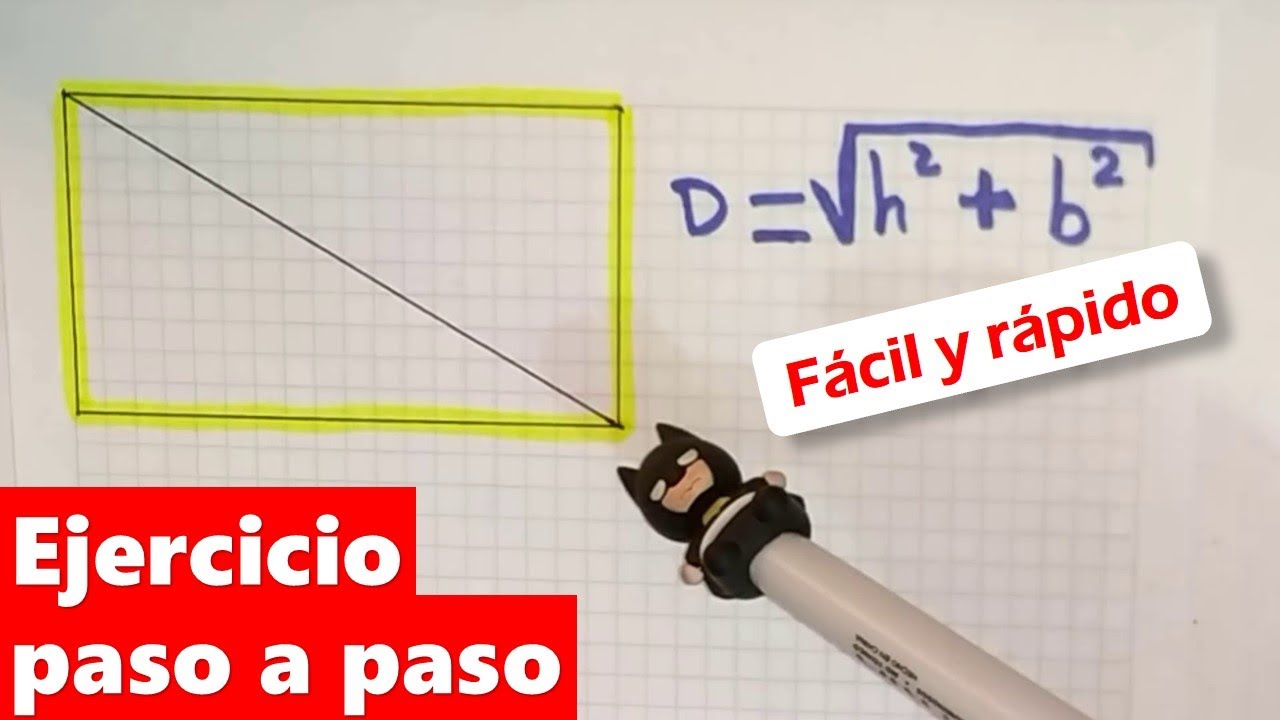
Source: Youtube.com
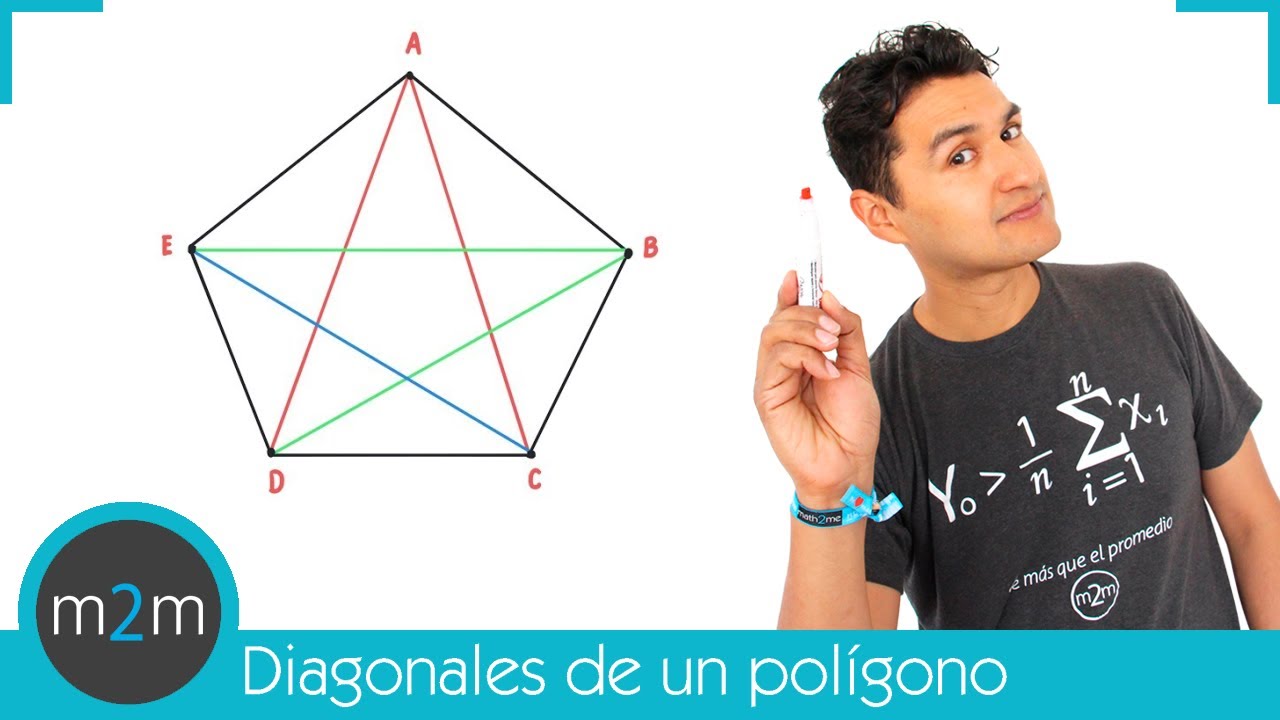
Cantidad de DIAGONALES de un POLÍGONO – BUENISIMO
Source: Youtube.com