
En álgebra, la palabra "diagonal" tiene dos significados principales:
- En geometría, una diagonal es un segmento que une dos vértices no consecutivos de un polígono o de un poliedro.
- En matrices, una matriz diagonal es una matriz cuadrada en la que todos los elementos fuera de la diagonal principal son iguales a cero.
En esta publicación de blog, exploraremos ambos significados de la palabra "diagonal" en álgebra.
Diagonales en geometría
En geometría, una diagonal es un segmento que une dos vértices no consecutivos de un polígono o de un poliedro. Por ejemplo, en el triángulo de la derecha, las diagonales son AB y AC.
[Imagen de un triángulo con diagonales AB y AC]
El número de diagonales que se pueden trazar en un polígono depende del número de lados del polígono. En general, el número de diagonales de un polígono de n lados se puede calcular con la siguiente fórmula:
n(n-3)/2 Por ejemplo, un triángulo tiene 3 lados, por lo que el número de diagonales que se pueden trazar es (3)(3-3)/2 = 0. Un cuadrilátero tiene 4 lados, por lo que el número de diagonales que se pueden trazar es (4)(4-3)/2 = 2. Un pentágono tiene 5 lados, por lo que el número de diagonales que se pueden trazar es (5)(5-3)/2 = 5.
Diagonales en matrices
En matrices, una matriz diagonal es una matriz cuadrada en la que todos los elementos fuera de la diagonal principal son iguales a cero. Por ejemplo, la siguiente matriz es una matriz diagonal:
A = [ 1 0 0 0 2 0 0 0 3 ] En esta matriz, los elementos de la diagonal principal son 1, 2 y 3, y todos los demás elementos son 0.
Las matrices diagonales tienen muchas propiedades interesantes. Por ejemplo, el determinante de una matriz diagonal es igual al producto de los elementos de la diagonal principal. Además, el rango de una matriz diagonal es igual al número de elementos no nulos de la diagonal principal.
Aplicaciones de las diagonales
Las diagonales se utilizan en muchas áreas de las matemáticas y la ciencia. Por ejemplo, las diagonales se utilizan en geometría para calcular el área y el perímetro de polígonos. También se utilizan en álgebra para calcular el determinante y el rango de matrices.
Las diagonales también se utilizan en otras áreas, como la física, la ingeniería y la informática. Por ejemplo, las diagonales se utilizan en la teoría de grafos para estudiar las conexiones entre los vértices de un grafo. También se utilizan en la teoría de matrices para estudiar las propiedades de las matrices diagonales.
Conclusión
En álgebra, la palabra "diagonal" tiene dos significados principales:
- En geometría, una diagonal es un segmento que une dos vértices no consecutivos de un polígono o de un poliedro.
- En matrices, una matriz diagonal es una matriz cuadrada en la que todos los elementos fuera de la diagonal principal son iguales a cero.
Las diagonales se utilizan en muchas áreas de las matemáticas y la ciencia, y tienen muchas propiedades interesantes.
-
diagonal
-
geometría
-
matriz
-
diagonal principal
-
determinante
-
rango
-
polígono
-
poliedro
-
grafo
-
teoría de matrices
-
triángulo
-
cuadrilátero
-
pentágono
-
1
-
2
-
3
-
0
-
área
-
perímetro
-
grafo
Diagonal Matrix – Definition, Inverse | Diagonalization

Source: Cuemath
Diagonal Matrix Definition, examples and its properties

Source: BYJU'S
Diagonal of Rectangle Formula – What is Diagonal of Rectangle Formula? Examples

Source: Cuemath
Que Es Diagonal En Algebra, ALGEBRA Matriz Diagonal UNIVERSIDAD unicoos matematicas diagonalizacion, 7.9 MB, 05:45, 495,623, unicoos, 2014-01-29T16:26:22.000000Z, 2, Diagonal Matrix – Definition, Inverse | Diagonalization, Cuemath, 559 x 695, jpg, , 3, que-es-diagonal-en-algebra, KAMPION
Que Es Diagonal En Algebra.
Si este video te ayuda y quieres que unicoos siga creciendo, SUSCRÍBETE, haz click en “Me gusta” y COMPÁRTELO. Si también te sumas a nosotros en unicoos.com será la bomba!!! #nosvemosenclase 🙂
Correspondiente a ALGEBRA universitaria, haremos un ejercicio de DIAGONALIZACION de MATRICES. Basandonos en el Teorema de CAYLEY-HAMILTON, | A-λ.I | = 0, obtendremos el POLINOMIO CARACTERISTICO de una matriz y despues sus VALORES PROPIOS o AUTOVALORES. Una vez conocidos éstos, hallaremos tres matrices diagonales semejantes a ella. Os dejo también el link del vídeo en el que termino el ejercicio y obtengo los VECTORES PROPIOS de la MATRIZ youtube.com/watch?v=dUdS6alENbY
Puedes encontrar otros vídeos de ÁLGEBRA universitaria en esta sección de la web… unicoos.com/asignaturas/matematicas/universidad/6/algebra/37/
“Snowflake – Longing (Base Mode pres. Lunar Chillout Mix)” by Lunar
ccmixter.org/files/lunarmusic/37560 is licensed under a Creative Commons license: creativecommons.org/licenses/by/3.0/
Síguenos en:
YOUTUBE youtube.com/unicoos
FACEBOOK facebook.com/unicoos (Me gusta)
TWITTER twitter.com/unicoos (@unicoos)
GOOGLE + google.com/+unicoos
WEB unicoos.com
Y si quieres ayudarme a subtitular los vídeos a otros idiomas, te lo agradeceré infinito… amara.org/es/profiles/videos/unicoos/
Diagonal Matrix – Definition, Inverse | Diagonalization
ALGEBRA Matriz Diagonal UNIVERSIDAD unicoos matematicas diagonalizacion

Source: Youtube.com
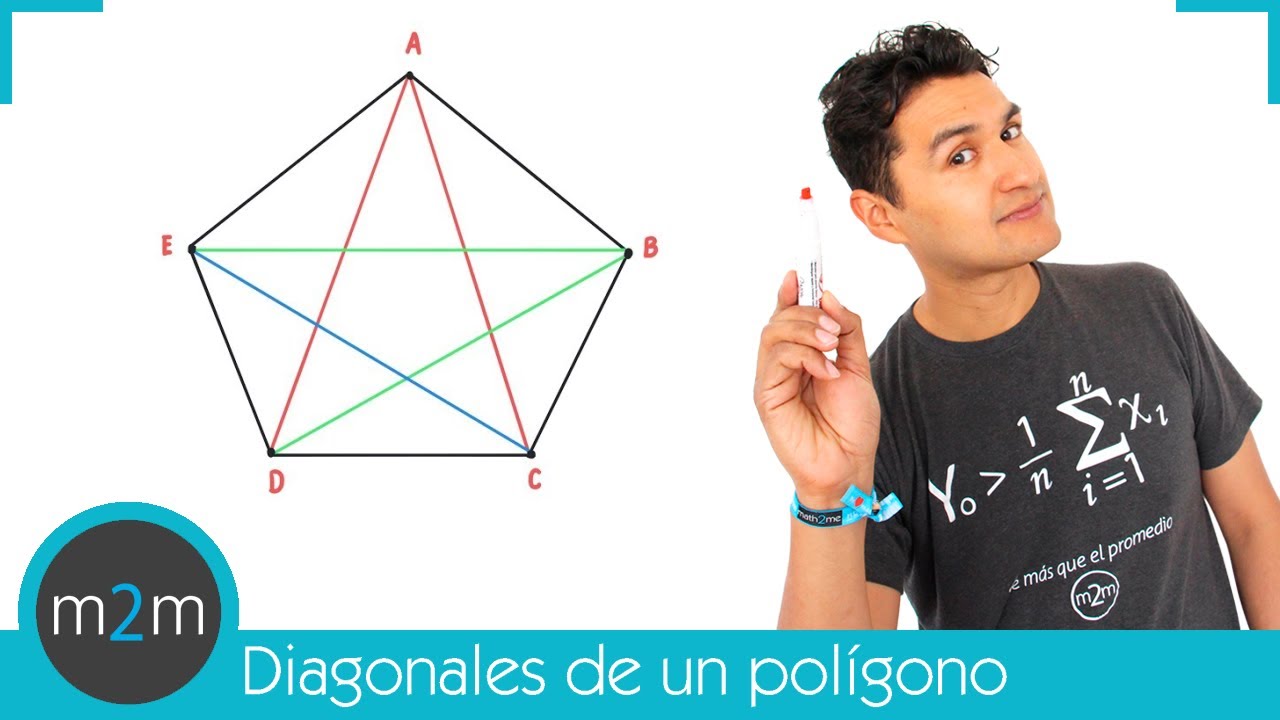
Cantidad de DIAGONALES de un POLÍGONO – BUENISIMO
Source: Youtube.com